Question

In Young’s double slit experiment, the two slits are $d$ distance apart. Interference pattern is observed on a screen at a distance $D$ from the slits. A dark fringe is observed on the screen directly opposite to one of the slits. The wavelength of the light is
$A)\text{ }\dfrac{{{D}^{2}}}{2d}$
$B)\text{ }\dfrac{{{d}^{2}}}{2D}$
$C)\text{ }\dfrac{{{D}^{2}}}{d}$
$D)\text{ }\dfrac{{{d}^{2}}}{D}$

Answer 1

- Hint: This problem can be solved by using the direct formula for the path difference between the two rays in a Young’s Double Slit Experiment in terms of the separation between the slits and the distance to the screen and combining it with the direct formula for the path difference between two rays for destructive interference in terms of the wavelength.

Formula used:
$\Delta x=d\dfrac{y}{D}$
$\Delta x=\left( n+\dfrac{1}{2} \right)\lambda$

Complete step-by-step solution:
In a Young’s double slit experiment, the path difference $\Delta x$ between the two light rays emanating from the slits and meeting at a point on the screen is given by
$\Delta x=d\dfrac{y}{D}$ --(1)
Where $d$ is the separation between the slits, $y$ is the vertical distance from the midpoint of the separation of the slits to the point on the axis where the rays meet and $D$ is the distance of the screen from the slits.
The path difference $\Delta x$ between two waves which interfere destructively is given by
$\Delta x=\left( n+\dfrac{1}{2} \right)\lambda$ $\left( n=0,1,2... \right)$ --(2)
Where $\lambda$ is the wavelength of the waves.
Now, let us analyze the question.

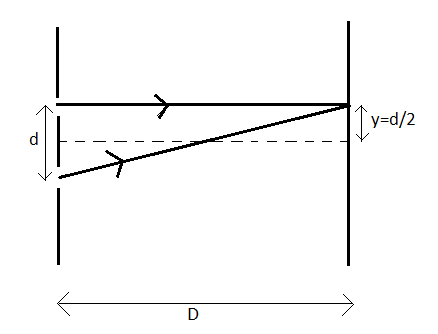
The separation between the slits is given to be $d$.
The distance of the screen from the slits is given to be $D$.
Let the vertical distance of the point where the two light rays emanating from the slits meet on the screen, from the midpoint of the separation between the slits be $y$.
Let the wavelength of the light used be $\lambda$.
Let the path difference between the two light rays emanating from the slits and meeting on the screen be $\Delta x$.
Now, it is given that the required point of meeting of the rays on the screen is opposite to one of the slits.
Therefore, the vertical distance of the point from the midpoint of the separation between the slits will be nothing but half of the separation between the slits.
$\therefore y=\dfrac{1}{2}d$ --(3)
Also, using (1), we get
$\Delta x=d\dfrac{y}{D}$ --(4)
Now, for dark fringes, there must be destructive interference between the two light rays.
Therefore, using (2), we get
$\Delta x=\left( n+\dfrac{1}{2} \right)\lambda$ --(5)
Equating (4) and (5), we get
$d\dfrac{y}{D}=\left( n+\dfrac{1}{2} \right)\lambda$ --(6)
Putting (3) in (6), we get
$d\dfrac{\dfrac{1}{2}d}{D}=\left( n+\dfrac{1}{2} \right)\lambda$
$\therefore \dfrac{{{d}^{2}}}{2D}=\left( n+\dfrac{1}{2} \right)\lambda$
Considering $n=0$, that is, if we consider the first dark fringe, we get
$\therefore \dfrac{{{d}^{2}}}{2D}=\left( 0+\dfrac{1}{2} \right)\lambda =\dfrac{1}{2}\lambda$
$\therefore \lambda =\dfrac{{{d}^{2}}}{2D}\times 2=\dfrac{{{d}^{2}}}{D}$
Hence, we have got the required expression for the wavelength of the light.
Therefore, the correct option is $D)\text{ }\dfrac{{{d}^{2}}}{D}$.

Note: Though in the question, it is not mentioned that the dark fringe is the first one, we have considered it to be so to get an answer that matches one of the options. Students must take note that the expression for the wavelength will change depending upon the number of the dark fringe that is formed. They must also take note that the wavelength will also depend upon the medium that the experiment is conducted in. If the experiment is conducted in another medium with a different refractive index, the wavelength and hence, the positions of the fringes will change accordingly.