Solveeit Logo
Login

Question

Question: In Young’s double slit experiment, the distance between two sources is 0.1mm. The distance of the sc...

In Young’s double slit experiment, the distance between two sources is 0.1mm. The distance of the screen from the sources is 20cm. Wavelength of the light used is 5460A∘5460A{}^\circ . Then angular position of the first dark fringe is
A. 0.08∘0.08{}^\circ
B. 0.16∘0.16{}^\circ
C. 0.20∘0.20{}^\circ
D. 0.313∘0.313{}^\circ

Explanation

Solution

First of all, note down all the given quantities in their SI units. You could then recall the expression for the nth dark fringe for a Young’s double slit experiment. In that expression, you could substitute one for the value of n and after that all the other values given and thus find the answer.

Formula used:
Angular position,
θn=(2n−1)λ2d{{\theta }_{n}}=\left( 2n-1 \right)\dfrac{\lambda }{2d}

Complete Step by step solution:
In the question we are given certain values related to Young’s double slit experiment. The distances between the sources is given by,
d=0.1mm=0.1×10−3md=0.1mm=0.1\times {{10}^{-3}}m

The distance between the screen and the source is given by,
D=20×10−2mD=20\times {{10}^{-2}}m

The wavelength of the light being used for the experiment is given as,
λ=5460A∘\lambda =5460A{}^\circ

Using all these information, we are supposed to find the angular position of the first dark fringe.

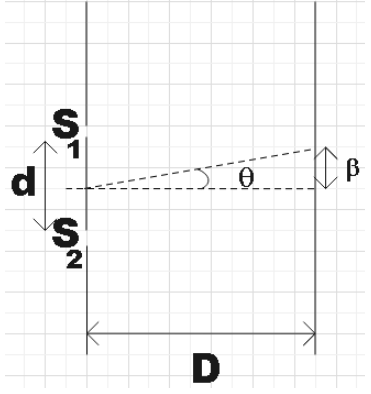
Let us recall the expression for finding the angular position of nth dark fringe in the interference pattern.
θn=(2n−1)λ2d{{\theta }_{n}}=\left( 2n-1 \right)\dfrac{\lambda }{2d}

Now, for the first dark fringe, n=1, so, the expression will now become,
θ1=λ2d{{\theta }_{1}}=\dfrac{\lambda }{2d}

Now, we could substitute the given values to get,
θ1=5460×10−102×0.1×10−3{{\theta }_{1}}=\dfrac{5460\times {{10}^{-10}}}{2\times 0.1\times {{10}^{-3}}}
⇒θ1=2730×10−6rad\Rightarrow {{\theta }_{1}}=2730\times {{10}^{-6}}rad

Since the options are given in degrees, let us convert the value.
θ1=2730×10−6×180π{{\theta }_{1}}=2730\times {{10}^{-6}}\times \dfrac{180}{\pi }
∴θ1=0.16∘\therefore {{\theta }_{1}}=0.16{}^\circ

Therefore, we found the angular position of the first dark fringe to be 0.16∘0.16{}^\circ .

Hence, option B is found to be the correct answer.

Note:
You may see that the angular position of the first dark fringe is independent of the distance between the screen and the source (D). From the figure we see that,
θ=βD\theta =\dfrac{\beta }{D}
Substituting the expression for the fringe widthβ\beta , we get,
θ=λD2dD=λ2d\theta =\dfrac{\lambda D}{2dD}=\dfrac{\lambda }{2d}
This is how we have arrived at the expression used in the solution. (2n-1) is used to indicate the odd number of fringe.