Question

In Young’s double-slit experiment, the angular width of a fringe formed on a distant screen is ${1^0}.$ The wavelength of light used is $6000{A^0}.$ What is the spacing between the slits?
(A). 344mm
(B). 0.1344mm
(C). 0.0344mm
(D). 0.034mm

Answer 1

Hint: To deal with these types of questions first we will understand the concept of Young’s Double slit experiment which uses two coherent sources of light placed at a small distance apart and then we will use the required formula to solve the question.
Formula Used: $y = \dfrac{{D\lambda }}{d}$
Where,
$\lambda = {\text{ wavelength }} \\\ d = {\text{distance between the slits}} \\\ D = {\text{separation between the screen}} \\\$

Complete step-by-step solution -

The wavelength of the light is 6000A and the angular width of the fringe on the screen is 1 degree.

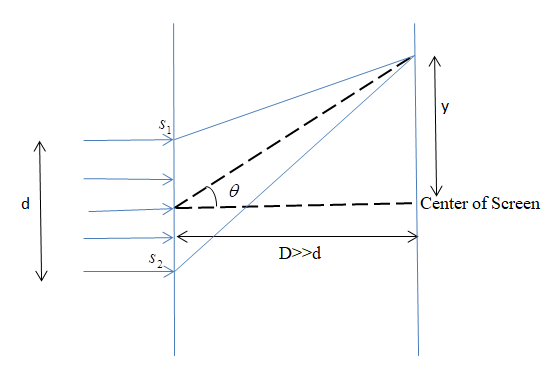
Using the formula given above for calculating the value of d
$\Rightarrow y = \dfrac{{D\lambda }}{d} \\\ \Rightarrow \dfrac{y}{D} = \dfrac{\lambda }{d}.....................................(1) \\\$
From the figure given above, we will find the value of $\theta$
As we know that $\left[ {\tan \theta = \dfrac{{{\text{perpendicular}}}}{{{\text{base}}}}} \right]$
$\Rightarrow \tan \theta = \dfrac{y}{D}.............(2)$
Also, for small angle when angle is very less
Then $\sin \theta = \tan \theta = \theta \left( {radian} \right)...........(3)$
Now, using equation (1), (2) and (3) we get
$\Rightarrow \dfrac{y}{D} = \sin \theta = \tan \theta = \theta \\\ \Rightarrow \theta = \dfrac{\lambda }{d} \\\$
Now, substituting the value of wavelength and angle from the data given in the question
$\Rightarrow \dfrac{\pi }{{{{180}^0}}} = \dfrac{{6000{A^0}}}{d} \\\ \Rightarrow d = \dfrac{{6000 \times {{10}^{ - 10}} \times 180}}{{3.14}} \\\$
After further simplification, we get
$\Rightarrow d = 0.034mm$
Hence the space between the slits is 0.034mm and the correct option is D.

Note- Young’s double slit experiment is just demonstration of wave behavior of light by showing constructive and destructive interferences (property of wave) on the screen. Also for the double-slit geometry, an important parameter is the ratio of the light's wavelength to the slits spacing d. When $y/d$ is much less than 1, the distance between successive fringes of interference may be high, and the results of interference may not be detectable. Young attempted to isolate the interference fringes using narrowly separated slits.