Question

In Young's double slit experiment, the distance between slits and the screen is 1.0m and monochromatic light of 600nm is being used. A person standing near the slits is looking at the fringe pattern. When the separation between the slits is varied, the interference pattern disappears for a particular distance ${{d}_{0}}$ between the slits. If the angular resolution of the eye is $\dfrac{1}{60}$​, the value of d0​ is close to:
A. 3 mm
B. 4 mm
C. 1 mm
D. 2 mm

Answer 1

we are given the distance between the slit and screen and the wavelength of the monochromatic light used in a Young’s double slit experiment. It is said that for a person observing the fringe pattern in the vicinity of the slits, the fringe pattern disappears for a particular distance between the slits. We are also given the angular resolution of his eye, i.e. the angle after which he cannot see the fringe pattern. We have an equation for fringe width, by using this equation we can find the solution.
Formula used:
$\beta =\dfrac{\lambda D}{d}$

Complete answer:
In the question we are given a Young’s double slit experiment.
We are given the distance between the slits and the screen as 1.0 m and the wavelength of the monochromatic light used as 600 nm.
It is said that a person is looking at the fringe pattern by standing near the slits and at a particular distance ${{d}_{0}}$ the fringe pattern disappears.
The angular resolution of eye is given to us as $\dfrac{1}{60}$
The figure below shows us the given situation.

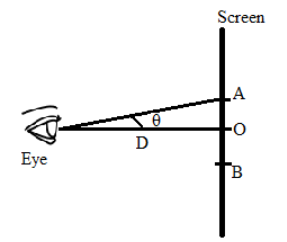
Here ‘O’ is the central maxima and the distance AO and OB is known as the fringe width.
We know that the person is viewing from near the slits. Therefore the distance between the person and the screen is the distance between the slit and the screen which is given as 1.0 m.
The angle made by the eye and the fringe is taken as ‘$\theta$’.
Now we know that the equation for fringe width is given as,
$\beta =\dfrac{\lambda D}{d}$, here ‘$\lambda$’ is the wavelength of the light, ‘D’ is the distance between slit and screen, ‘d’ is the distance between the slits.
From the figure we can see that,
$\tan \theta =\dfrac{AO}{D}$
We know that AO is the fringe with and also for small angles ‘$\theta$’, $\tan \theta \simeq \theta$.
Therefore we can write this equation as,
$\theta =\dfrac{\beta }{D}$
From the equation for fringe width we can see that,
$\dfrac{\beta }{D}=\dfrac{\lambda }{d}$
Therefore we get,
$\Rightarrow \theta =\dfrac{\lambda }{d}$
In the question we are given that the angular resolution of the eye is ${{\left( \dfrac{1}{60} \right)}^{o}}$. From this we can understand that ${{\left( \dfrac{1}{60} \right)}^{o}}$ is the minimum angle that the person can see the fringes.
Therefore we have,
$\theta ={{\left( \dfrac{1}{60} \right)}^{o}}$ by converting this into radians, we get,
$\Rightarrow \theta =\dfrac{1}{60}\times \dfrac{\pi }{180}rad$
Since $\theta =\dfrac{\lambda }{d}$, we can write,
$\Rightarrow \dfrac{\lambda }{d}=\dfrac{\pi }{60\times 180}$
From this we can find d as,
$\Rightarrow d=\dfrac{60\times 180\times \lambda }{\pi }$
We know that wavelength of the monochromatic light used,
$\lambda =600nm=600\times {{10}^{-9}}m$
Therefore we get,
$\Rightarrow d=\dfrac{60\times 180\times 600\times {{10}^{-9}}}{\pi }$
By solving this we will get,
$\Rightarrow d=2.06\times {{10}^{-3}}m$
$\Rightarrow d\approx 2mm$
Since $\dfrac{\lambda }{d}=\theta$, we can say that as we increase ‘d’ the angular resolution will decrease, i.e. the person will not be able to see the fringes.
Therefore the maximum value of distance between the slits is 2 mm.

Hence the correct answer is option D.

Note:
Young’s double slit experiment helps us to prove the wave theory of light. By doing this experiment we can demonstrate the constructive and destructive interference. Constructive interference forms when the path difference of the lights from the two slits is an integral multiple of the wavelength of the light used in the experiment. Destructive interference occurs when the path difference is a half – integral multiple of the wavelength.