Question

In YDSE, the intensity of the maxima is I. If the width of each slit is doubled the intensity of the maxima will be:
$\begin{aligned} & \text{A}\text{. I/2} \\\ & \text{B}\text{. I} \\\ & \text{C}\text{. 4I} \\\ & \text{D}\text{. 2I} \\\ \end{aligned}$

Answer 1

Young's double slit experiment is a demonstration of both the wave nature and the particle nature of light. Express how the intensity of light rays varies with the slit width. Then, find the central maxima using the acquired values. Take the ratio to find the final intensity of the central maxima.

Complete step by step answer:

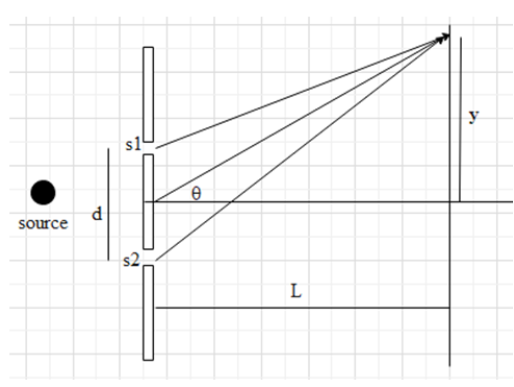
Let the intensity of light coming in from each slit in a young’s double slit experiment is ${{I}_{0}}$ .
Given that the intensity of the central maxima of the young’s double slit experiment is $I$ .
The total intensity of the interference pattern in a young’s double slit experiment is given as,
$I={{I}_{1}}+{{I}_{2}}+2\sqrt{{{I}_{1}}{{I}_{2}}}\cos \theta$
Here, we let that both the light rays from each slit have the same intensity ${{I}_{o}}$ and for the central maxima the value of $\cos \theta$ will be 1.
So, $\begin{aligned} & I={{I}_{0}}+{{I}_{0}}+2\sqrt{{{I}_{0}}{{I}_{0}}} \\\ & \Rightarrow I=4{{I}_{0}} \\\ \end{aligned}$
Now, the intensity of the light ray coming from slits depends on the slit width. The intensity of the light ray is directly proportional to the slit width.
Given in the question, that the slit width of each slit in the young’s double slit experiment is doubled. Since, the intensity is proportional to the slit width, the intensity of the light ray will also be doubled.
So, now the intensity of the light ray from each slit will be, $2{{I}_{0}}$ .
So, the total intensity of the central maxima will be,
$\begin{aligned} & {{I}_{f}}=2{{I}_{0}}+2{{I}_{0}}+2\sqrt{2{{I}_{0}}\times 2{{I}_{0}}} \\\ & \Rightarrow {{I}_{f}}=8{{I}_{0}} \\\ \end{aligned}$
Taking the ratio of the above two,
$\begin{aligned} & \Rightarrow \dfrac{{{I}_{f}}}{I}=\dfrac{8{{I}_{0}}}{4{{I}_{0}}} \\\ & \dfrac{\Rightarrow {{I}_{f}}}{I}=2 \\\ & \therefore {{I}_{f}}=2I \\\ \end{aligned}$

So, the correct answer is “Option D”.

Note:
In a young’s double slit experiment we get an interference pattern with constructive interference and destructive interference. For the central maxima we will get the maximum intensity and after that the intensity will gradually decrease in both sides of the central maxima.