Question

In which quadrant does the graph of $- 1 - 2i$ lie?

Answer 1

To solve this question first we make a complex plane indicating a real and complex plane. Then first we indicate the real part and then we plot the imaginary part then we make two lines parallel and perpendicular to both the axis passing through the points. Then we observe the point and find the quadrant of that point.

Complete step-by-step answer:
In this question, we have to find the quadrant in which the graph of $- 1 - 2i$ lies.
Using the concept of a complex plane and plotting the real part along the x-axis and imaginary along the y-axis.
Now first we plot the real part that is $- 1$.
The real part is 1 unit on the left side of the intersection of the real and imaginary parts.
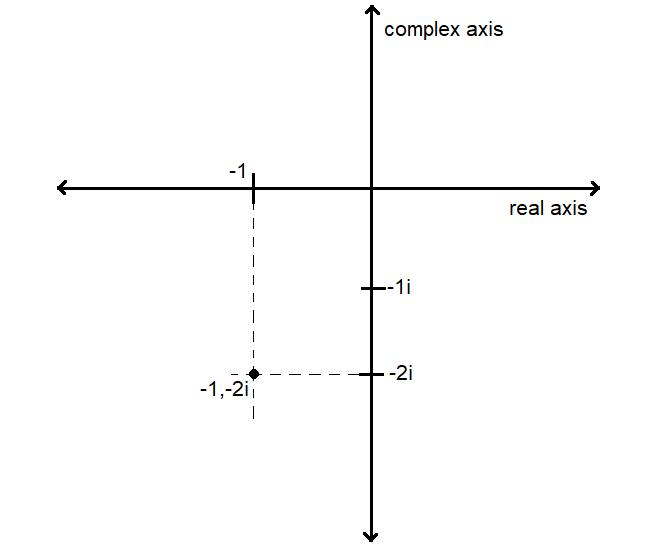Now we plot the imaginary part that is $- 2i$.
The imaginary part is 2 units below the intersection of the real and imaginary part.
Then we make a line parallel to the y-axis passing through the real part. And a line parallel to the x-axis passing through the imaginary part.
The point of intersection gives the point which we have to indicate of the complex plane.
The graph of the point is shown in fig.
Now we observe that the point is lying in the third quadrant.
Final answer:
The graph of $- 1 - 2i$ lying in the third quadrant.

Note: Although this question is easy. But students must know how they plot the graph of complex numbers. Students often make mistakes in plotting the number only. The graph is also made directly but students get marks if they do that step by step solution.