Question
Question: In which position (A, B, C, or D) of the second charge, the flux of the electric field through the h...
In which position (A, B, C, or D) of the second charge, the flux of the electric field through the hemisphere remains uncharged? Explain.
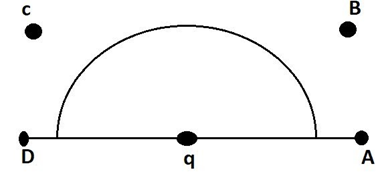
Solution
First we need to draw the diagram of the charge that is radiating from ‘q’. After doing this we have to place the charge at each of the points that is A, B, C, D. And check that the electric field line crossing the surface is twice or once.
Formula Used:
ϕ=E.ds
ϕ=E.dscosθ
Complete step by step answer:
In the diagram that is given in the question we see, a charge ‘q’ is placed at the center of the hemisphere. And if we consider a second charge ‘Q’ is placed at one of the points A, B, C, D respectively then the flux of the electric field through the hemisphere remains un-charged at any of the points.
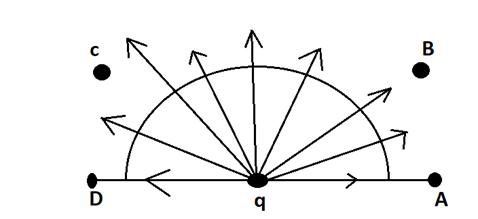
Now, if we consider the charge ‘q’ as a positive charge, then we know that the positive field line always radiates outwards from the positive charge then the representation of the line is shown in the diagram.
We know that electric flux is the total number of electric field lines passing perpendicular to the surface.
Now, if we place the charge ‘Q’ at point D then,

We can see in the above diagram when the charge ‘Q’ is placed at D then any of the field lines are passing the surface twice, so the net influence of the charge will be zero.
We will see the same thing happening if the charge ‘Q’ is placed on point A also.
Now, if we place the charge at point ‘C’ or ‘B’
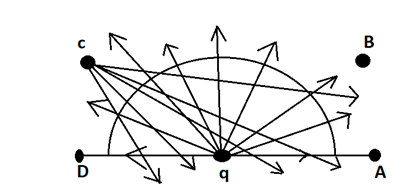
Then we can see that some of the lines are passing the surface twice but there are also lines which are passing through the surface once only, so for the line passing the surface twice there will be no difference but for the lines passing the surface once they will bring the difference to the flux. And there will be a net influence on the flux.
We know that we calculate flux, by the formula
ϕ=E.ds or ϕ=E.dscosθ,
Now this, θ, is the angle that the flux is making with the area vector. And if we calculate the net flux for those lines radiating twice we will see that the flux will be the same with the opposite sign that is one will be positive another one will be negative. So, as a result, they will cancel out each other.
Note:
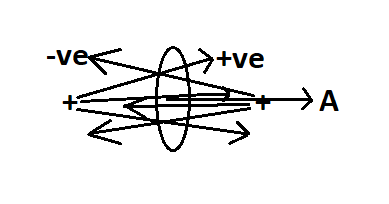
If we consider two charges at both ends of the surface then their electric field lines must be like shown in the above figure. Now according to the ampere’s circuital law, we must define an area vector in a particular direction which we have considered as ‘A’. Now the field line which is traveling in the direction of area vector those are considered as positive field lines and the line traveling opposite to the area vector then they are considered negative field lines. And the net charge passing through the surface is the subtraction of positive charge and negative charge respectively.
