Question

In which direction should a motorboat head in order to reach a point on the opposite bank directly east from the starting point? (The boat's speed relative to the water remains $4m{{s}^{-1}}$, velocity of river relative to ground is $2m{{s}^{-1}}$)

Answer 1

As motor boats have to reach at the exact opposite end of the river it will have to move somewhat opposite to the direction of flow of the river. The component of velocity along the direction opposite to flow of the river must be zero. This condition can be used to obtain the direction a motorboat should head to reach at an exactly opposite point.

Complete step-by-step answer:
As motor boats have to reach at the exact opposite end of the river it will have to move somewhat opposite to the direction of flow of the river. Let us assume that the motor boat has to head at an angle $\theta$ with the direction opposite to the flow of the water. The boat is moving with a velocity of $4m{{s}^{-1}}$ with respect to that of water.

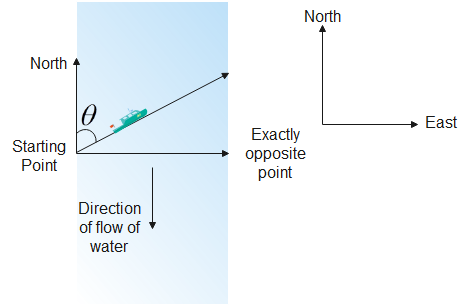
Relative velocity of a body is defined as the velocity of that body with reference to some other body assumed to be at rest. Here, the relative velocity of the motor boat is given with respect to water. That is,
${{v}_{b,w}}={{v}_{b,g}}-{{v}_{w,g}}$
Where ${{v}_{b,w}}$, ${{v}_{b,g}}$ and ${{v}_{w,g}}$ are velocity of boat with respect to water, velocity of boat with respect to ground and velocity of water relative to ground respectively.
Since motor boats have to reach at the exact opposite end of the river, its component parallel to flow of water is equal to velocity of water with respect to ground in magnitude but opposite in direction. Therefore, ${{v}_{b,w}}\cos \theta ={{v}_{w,g}}$
Given that, ${{v}_{b,w}}=4m/s$ and ${{v}_{w,g}}=2m/s$. Substituting these values, we have
$4\cos \theta =2$
This implies that,
$\cos \theta =\dfrac{1}{2}$
We know that, $\cos \theta =\dfrac{1}{2}$ for $\theta ={{60}^{{}^\circ }}$
Hence, the motorboat should head in ${{60}^{{}^\circ }}$ east of north.

So, the correct answer is “Option A”.

Note: Velocity is a vector quantity and has both magnitude and direction.
The relative velocity of an object A with respect to B is defined as its velocity in the rest frame of object B.
For a motor boat to reach at the exact opposite end of the river it will have to move somewhat aiming to opposite the direction of flow of the river.