Question

In what ratio is the line segment joining the points (-3, 2) and (6, 1) is divided by y – axis?
A. $1:3$
B. $2:1$
C. $1:2$
D. $3:1$

Answer 1

Hint: Consider any point on the y – axis of the form $\left( 0,a \right)$. Assume that this point divides the points $\left( -3,2 \right)$ and $\left( 6,1 \right)$ in the ratio $m:1$. Use the section formula for finding the coordinates of points which divides two points $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ in the ratio $u:v$.

Complete step-by-step answer:
We have two points $\left( -3,2 \right)$ and $\left( 6,1 \right)$. We have to find the ratio in which line joining these two points is divided by the y – axis.
Let’s assume that the point on the y – axis is of the form $\left( 0,a \right)$. Let’s assume that the point $\left( 0,a \right)$ divides the line joining $\left( -3,2 \right)$ and $\left( 6,1 \right)$ in the ratio $m:1$.

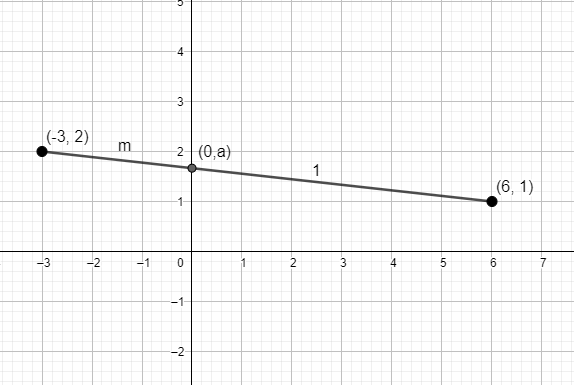
We will now use section formula to find the value of m. We know that the co-ordinates of point dividing two points $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ in the ratio $u:v$ is $\left( \dfrac{{{x}_{1}}v+{{x}_{2}}u}{u+v},\dfrac{{{y}_{1}}v+{{y}_{2}}u}{u+v} \right)$.
Substituting ${{x}_{1}}=-3,{{x}_{2}}=6,{{y}_{1}}=2,{{y}_{2}}=1,u=m,v=1$ in the above equation, the co-ordinates of point dividing $\left( -3,2 \right)$ and $\left( 6,1 \right)$ in the ratio $m:1$ is $\left( \dfrac{-3\left( 1 \right)+6m}{m+1},\dfrac{2\left( 1 \right)+m}{m+1} \right)$.
However, we know that the co-ordinates of point dividing $\left( -3,2 \right)$ and $\left( 6,1 \right)$ in the ratio $m:1$ is $\left( 0,a \right)$.
Thus, we have $\left( 0,a \right)=\left( \dfrac{-3\left( 1 \right)+6m}{m+1},\dfrac{2\left( 1 \right)+m}{m+1} \right)$.
By equation terms , we have $0=\dfrac{-3+6m}{m+1},a=\dfrac{2+m}{m+1}$.
Solving the equation $0=\dfrac{-3+6m}{m+1}$ by cross multiplying the terms, we have $-3+6m=0$.
Thus, we have $m=\dfrac{1}{2}$.
Hence, the ratio in which the line joining $\left( -3,2 \right)$ and $\left( 6,1 \right)$ is divided by y – axis is $m:1=\dfrac{1}{2}:1=1:2$, which is option (c).

Note: We don’t have to find the exact coordinates of the point on the y – axis which divides the points. However, if we wish to do so, we can substitute the value of m in the other equation and find the value of a. Section formula tells us the coordinates of the point which divides a given line segment with two end points in a fixed ratio.