Question

In what ratio is the line joining $\text{A}\left( 8,9 \right)$ and $\text{B}\left( -7,4 \right)$ is divided by
(a). The point $\left( 2,7 \right)$
(b). The x-axis
(c). The y-axis

Answer 1

Hint: suppose, the ratio in all cases lying on the line joining given as $k:1$. Use sectional formula given for calculating a point which divides the line segment joining the points $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$in the ratio $m:n$; point given as $\left( \dfrac{m{{x}_{2}}+n{{x}_{1}}}{m+n},\dfrac{m{{y}_{2}}+n{{y}_{1}}}{m+n} \right)$ any point on x-axis has y-coordinates as 0 and vice-versa is also true. Use this logic to solve the problem.

Complete step-by-step answer:

We know the point which divides the line joining the points $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ in ratio of $m:n$, is given by sectional formula as:-

$\text{R}\ =\ \left( \dfrac{m{{x}_{2}}+n{{x}_{1}}}{m+n},\dfrac{m{{y}_{2}}+n{{y}_{1}}}{m+n} \right)$ …………………………………………(i)
Now, coming to the question, we need to find the ratio by which line joining $\text{A}\left( 8,9 \right)$ and $\text{B}\left( -7,4 \right)$ would be divided by the given points in the axis.
(a). The point $\left( 2,7 \right)$
Let us suppose $\left( 2,7 \right)$ divides the line joining $\left( 8,9 \right)$and $\left( -7,4 \right)$ in ratio of $k:1$.

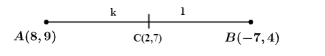
Now, we can get coordinates of c with the help of equation (i), where
$m=k$, $n=1$ and $\left( {{x}_{1}},{{y}_{1}} \right)\ =\ \left( 8,9 \right)$, $\left( {{x}_{2}},{{y}_{2}} \right)\ =\ \left( -7,4 \right)$
So, we get coordinated of c as
$c\ =\ \left( \dfrac{-7k+8}{k+1},\dfrac{4k+9}{k+1} \right)$
Now, it is given that coordinates of point c is $\left( 2,7 \right)$, So, we get,
$\dfrac{-7k+8}{k+1}\ =\ 2$ and $\dfrac{4k+9}{k+1}\ =\ 7$
$-7k+8\ =\ 2k+2$ and $4k+9\ =\ 7k+7$
$9k\ =\ 6$ and $3k\ =\ 2$
$k\ =\ \dfrac{6}{9}\ =\ \dfrac{2}{3}$ and $k\ =\ \dfrac{2}{3}$
Hence, ratio $k:1$is given as $2:3$.
So, point $\left( 2,7 \right)$ will divide the line joining the given points in ratio of $2:3$.
(b). The x- axis
Let us suppose that any coordinate on the x-axis will divide the line joining the given points in ratio $k:1$.

Let us suppose the point on the x-axis is represented by ‘c’.
So, coordinates of c can be given with the help of equation (i) as
$c\ =\ \left( \dfrac{-7k+8}{k+1},\dfrac{4k+9}{k+1} \right)$
As, the point c is lying on the x-axis, so y-coordinate of this point should be 0 because y-coordinate of any point at x-axis is 0.
So, put the y-coordinate of point c to 0, to get the value of k.
So, we get
$\dfrac{4k+9}{k+1}\ =\ 0$
Or $4k+9\ =\ 0$
$k\ =\ -\dfrac{9}{4}$
Hence, line joining by the point given points will be divided by x-axis in ratio of $9:4$ externally as the value of k is negative.
(c). The y-axis
So, we can use the previous coordinate of ‘c’. and put the x-coordinate of point c to 0, as x-coordinate on y-axis will be 0.
Hence, we get
$\dfrac{-7k+8}{k+1}\ =\ 0$
$-7k+8\ =\ 0$
$7k\ =\ 8$
$k\ =\ \dfrac{8}{7}$
So, the y-axis will divide the line joining the given points in ratio of $8:7$.

Note: please take care with the positions of $\left( {{x}_{1}},{{y}_{1}} \right)$, $\left( {{x}_{2}},{{y}_{2}} \right)$ and m and n in the sectional formula. One may go wrong if he/she applies this formula as $\left( \dfrac{m{{x}_{2}}+n{{x}_{1}}}{m+n},\dfrac{m{{y}_{2}}+n{{y}_{1}}}{m+n} \right)$ using the concept that x-coordinate of any point on y-axis is 0 and y-coordinate of any point on x-axis is 0 are the key points with the second and third party of the question.
Negative value of k suggests that the point dividing it in $k:1$ will not lie in between the line segments, it will divide the line externally, not internally.