Question

In what ratio is the line joining $\left( {2, - 4} \right)$ and $\left( { - 3,6} \right)$ divided by the y-axis?

Answer 1

We will take the point on the Y axis as (0,y). Then we will take the ratio that the line joining $\left( {2, - 4} \right)$ and $\left( { - 3,6} \right)$ is divided by the y-axis to be $\lambda :1$ Then we will apply section formula for the y coordinates which is given by $\dfrac{{m{x_2} + n{x_1}}}{{m + n}} = x$ . Then we will solve for $\lambda$ to get the required ratio.

Complete step-by-step answer:

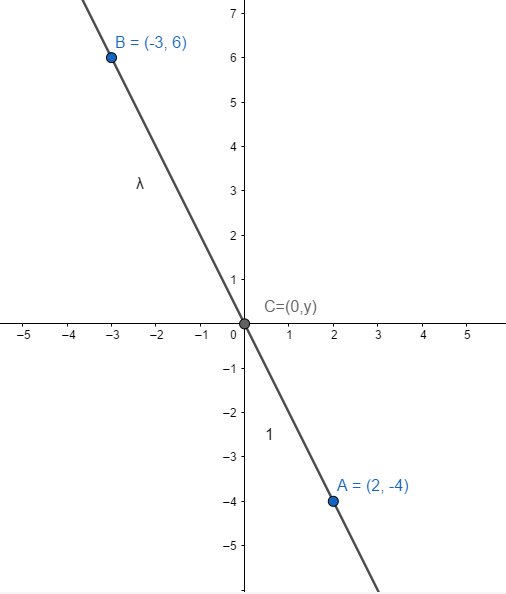
We are given the points A $\left( {2, - 4} \right)$ and B $\left( { - 3,6} \right)$ . We need to find the ratio that the y axis divides the line joining the given points.
Let the y axis divides the line in the ratio $\lambda :1$
By section formula, the coordinates of the point which divide the points $\left( {{x_1},{y_1}} \right)$ and $\left( {{x_2},{y_2}} \right)$ in the ratio $m:n$ is given by, $\left( {\dfrac{{m{x_2} + n{x_1}}}{{m + n}},\dfrac{{m{y_2} + n{y_1}}}{{m + n}}} \right)$
We know that any point on the y axis is given by (0,y). So, by applying section formula for the x coordinate, we can write,
$\dfrac{{m{x_2} + n{x_1}}}{{m + n}} = x$
On substituting the ratio $\lambda :1$ , we get,
$\Rightarrow \dfrac{{\lambda {x_2} + 1{x_1}}}{{\lambda + 1}} = x$
Now we can substitute the values of the x coordinates.
$\Rightarrow \dfrac{{\lambda \left( 2 \right) + 1\left( { - 3} \right)}}{{\lambda + 1}} = 0$
As the RHS is equal to zero, we can equate the numerator of the LHS to zero.
$\Rightarrow 2\lambda - 3 = 0$
$\Rightarrow 2\lambda = 3$
$\Rightarrow \lambda = \dfrac{3}{2}$
So, the required ratio is $\dfrac{3}{2}:1$
As we can multiply the ratio with the same number, we can multiply the ratio with 2.
$\Rightarrow \dfrac{3}{2}:1 = 3:1$
Therefore, the required ratio is $3:1$ .
Note: While taking the section formula, we must make sure that we take the ratio in the correct order. A way to remember the order is that we always multiply the ratio of one part with the coordinates of the point which is away from it. While taking the ratio we must take only it in the form $\lambda :1$ as it has only one variable and we can solve it easily. If we take the ratio as $m:n$ also, we can obtain the same answer. But it will be time consuming.