Solveeit Logo
Login

Question

Question: In \(\vartriangle \text{ABC}\), if a = 4b, b = 5, \(\angle \text{C = 60}{}^\circ \), then c =? (a)...

In △ABC\vartriangle \text{ABC}, if a = 4b, b = 5, ∠C = 60∘\angle \text{C = 60}{}^\circ , then c =?
(a) 5135\sqrt{13}
(b) 21\sqrt{21}
(c) 8
(d) 14

Explanation

Solution

In this question, first let us draw a triangle with the given conditions and then let us use the law of cosine formula when angle C is given along with two other sides, and to find the third side,c2=a2+b2−2ab⋅cosC{{\text{c}}^{2}}={{\text{a}}^{2}}+{{\text{b}}^{2}}-2\text{ab}\cdot \text{cosC}. Substitute in the formula and use simple mathematical operations to find the value of c.

Complete step-by-step answer:
Here first let us draw the triangle ABC with the conditions mentioned. Let us consider in the triangle ABC, we have side AB = a, side BC = b and side AC = c

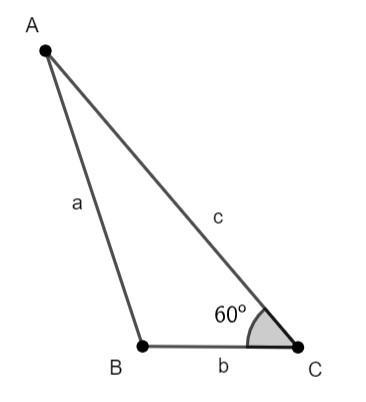
From the above diagram and given conditions we can see that, a = 4b and b = 5 and ∠C = 60∘\angle \text{C = 60}{}^\circ , let us find c.
Now if a = 4b and b = 5, we can say that a = 4(5) = 20.
We have to follow the law of cosines and use the formula c2=a2+b2−2ab⋅cosC{{\text{c}}^{2}}={{\text{a}}^{2}}+{{\text{b}}^{2}}-2\text{ab}\cdot \text{cosC}.
Now, after substituting the values in the above expression of cosine formula, we get
c2=(20)2+(5)2−2(20)(5)⋅cos⁡(60){{\text{c}}^{2}}={{\left( 20 \right)}^{2}}+{{\left( 5 \right)}^{2}}-2\left( 20 \right)\left( 5 \right)\cdot \cos \left( 60 \right)
We know, the value of cos⁡(60)=12\cos \left( 60 \right)=\dfrac{1}{2}
c2=400+25−2(20)(5)⋅12{{\text{c}}^{2}}=400+25-2\left( 20 \right)\left( 5 \right)\cdot \dfrac{1}{2}
=425−(20)(5) =425−100 =325\begin{aligned} & =425-\left( 20 \right)\left( 5 \right) \\\ & =425-100 \\\ & =325 \end{aligned}
Therefore, we got c2=325{{\text{c}}^{2}}=325
In the next step, let us take a square root on both the sides of the equation, we get
c2=325 c×c=5×5×13\begin{aligned} & \sqrt{{{\text{c}}^{2}}}=\sqrt{325} \\\ & \sqrt{\text{c}\times \text{c}}=\sqrt{5\times 5\times 13} \end{aligned}
Therefore, if we further simplify it, we will get the value of c.
c = 513\text{c = 5}\sqrt{13}
Therefore, the value of c = 5135\sqrt{13}.

So, the correct answer is “Option A”.

Note: Here, the Law of cosine states the relation between the lengths of sides of the given triangle with respect to the cosine of its angle. It is also known as the cosine rule. In order to find the value of a and b, we can use the formula a2=b2+c2−2bc⋅cos(A){{\text{a}}^{2}}={{\text{b}}^{2}}+{{\text{c}}^{2}}-2\text{bc}\cdot \text{cos}\left( \text{A} \right) and b2=a2+c2−2ac⋅cos(B){{\text{b}}^{2}}={{\text{a}}^{2}}+{{\text{c}}^{2}}-2\text{ac}\cdot \text{cos}\left( \text{B} \right) respectively.