Question

In $\vartriangle PQR$ right angled at Q, $PR + QR = 25{\text{ cm}}$ and $PQ = 5{\text{ cm}}$ . Determine the values of $\sin {\text{P}},\cos {\text{P}}$ and ${\text{tanP}}$ .

Answer 1

From the given equations we have the Pythagoras theorem to solve the above given equations as the given triangle is a right angled triangle. We will get the values of sides of the triangle. From the trigonometric formulae we can find the values of $\sin {\text{P}},\cos {\text{P}}$ and ${\text{tanP}}$ .

Complete step-by-step answer:
Given $\vartriangle PQR$ right angled at Q.

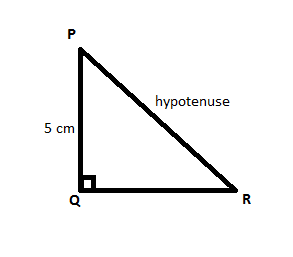
Right angled triangle is defined as a triangle in which one angle is a right angle. The relation between the sides and angles of a right triangle is the basis for trigonometry. The side opposite the right angle is called the hypotenuse. The sides adjacent to the right angle are called legs.
PQ+QR=25cm….(1)
PQ=5cm
By Pythagoras theorem,
${\text{P}}{{\text{Q}}^2} + {\text{Q}}{{\text{R}}^2} = {\text{P}}{{\text{R}}^2}$
Pythagoras theorem is a theorem attributed that the square the square on the hypotenuse of a right-angled triangle is equal in area to the sum of the squares on the other two sides
$\Rightarrow 25 = {\text{P}}{{\text{R}}^2} - {\text{Q}}{{\text{R}}^2}$
$\Rightarrow 25 = \left( {{\text{PR + QR}}} \right)\left( {{\text{PR - QR}}} \right)$
$\Rightarrow {\text{PR - QR = }}\dfrac{{25}}{{25}}$
$\Rightarrow {\text{PR - QR = 1}}$ … (2)
We now add (1) and (2)
$\Rightarrow 2{\text{PR = 26}}$
$\Rightarrow {\text{PR = 13}}$
Therefore, QR = 12 and PR = 13
Trigonometric values are based on three major trigonometric ratios, Sine, Cosine and Tangent. Sine or $\sin \theta$ = Side opposite to $\theta$ is to Hypotenuse. Cosines or $\operatorname{Cos} \theta$ = Adjacent side to $\theta$ is to Hypotenuse. Tangent or $\tan \theta$ = Side opposite to $\theta$ is to Adjacent side to $\theta$ .
$\Rightarrow \sin {\text{P = }}\dfrac{{{\text{QR}}}}{{{\text{PR}}}}$
$\Rightarrow \sin {\text{P = }}\dfrac{{12}}{{13}}$
And $\cos {\text{P = }}\dfrac{{{\text{PQ}}}}{{{\text{PR}}}}$
$\Rightarrow \cos {\text{P = }}\dfrac{5}{{13}}$
And ${\text{tan P = }}\dfrac{{\sin {\text{P}}}}{{\cos {\text{P}}}}$
$\Rightarrow {\text{tan P = }}\dfrac{{12}}{5}$

Note: There are six trigonometric ratios, sine, cosine, tangent, cotangent, secant and cosecant. We can find the remaining trigonometric ratios which are cotangent, secant and cosecant. Cotangent or $\cot \theta$ = Adjacent side to $\theta$ is to Side opposite to $\theta$ . Secant or $\operatorname{Sec} \theta$ = Hypotenuse is to Adjacent side to $\theta$ . Cosecant or $\operatorname{Cos} ec\theta$ = Hypotenuse is to Side opposite to $\theta$