Question

In $\vartriangle ABC$, M is the mid point of side QR. If PQ is $11cm$, PR is $17cm$ and QR is $12cm$, find PM.

Answer 1

For a better understanding always draw a figure first. This question can be easily solved by applying Apollonius theorem, $P{Q^2} + P{R^2} = 2P{M^2} + 2Q{M^2}$, and substituting the values.

Complete step-by-step answer:

 ![](https://www.vedantu.com/question-sets/c512441e-acec-4d9a-895a-225c4f9f6f3b6073128998478443768.png)  

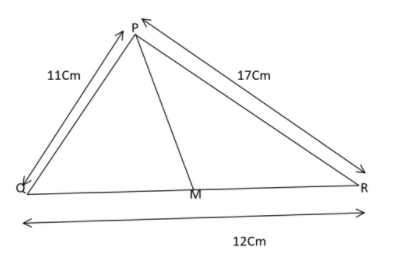
Given that M is the mid point of the side QR, i.e., PM is the median of the triangle.
Applying Apollonius theorem, which states that the sum of the squares of any two sides of a triangle equals twice the square on half the third side, together with twice the square on the median bisecting the third side. Hence, here it can be applied as:
$P{Q^2} + P{R^2} = 2P{M^2} + 2Q{M^2}$ (1)
Given that:
$PQ = 11cm \\\ PR = 17cm \\\ QR = 12cm \\\ QM + MR = QR \\\ QM = MR \\\$
(PM is the median)
$QM + QM = QR \\\ QM = \dfrac{{QR}}{2} \\\ QM = \dfrac{{12}}{2} = 6cm \\\$
Substituting the values of PQ, PR, QM in equation (1)
${11^2} + {17^2} = 2P{M^2} + 2{\left( 6 \right)^2} \\\ 121 + 289 = 2P{M^2} + 72 \\\ 410 = 2P{M^2} + 72 \\\ 2P{M^2} = 338 \\\ P{M^2} = 169 \\\ PM = 13cm \\\$

Note: The first approach to this type of problem is to always draw the figure first for a better and clear understanding. Then write down the things given and remember all the theorems you could apply to obtain the desired result.