Solveeit Logo
Login

Question

Question: In \(\vartriangle ABC\),\(\angle A = 90^\circ \), find\({\tan ^{ - 1}}\dfrac{b}{{a + c}} + {\tan ^{ ...

In △ABC\vartriangle ABC,∠A=90∘\angle A = 90^\circ , findtan⁡−1ba+c+tan⁡−1ca+b{\tan ^{ - 1}}\dfrac{b}{{a + c}} + {\tan ^{ - 1}}\dfrac{c}{{a + b}}

Explanation

Solution

Consider a, b, c as lengths of the sides of △ABC\vartriangle ABCsuch that a is the length of the side opposite to∠A=90∘\angle A = 90^\circ . Letx=ba+cx = \dfrac{b}{{a + c}}andy=ca+by = \dfrac{c}{{a + b}} . Then substitute for x and y in the inverse trigonometric formulatan⁡−1x+tan⁡−1y=tan⁡−1(x+y1−xy){\tan ^{ - 1}}x + {\tan ^{ - 1}}y = {\tan ^{ - 1}}(\dfrac{{x + y}}{{1 - xy}}). Simplify the expression using the Pythagoras’ theorem such that we get tan⁡−1ba+c+tan⁡−1ca+b=tan⁡−1(1){\tan ^{ - 1}}\dfrac{b}{{a + c}} + {\tan ^{ - 1}}\dfrac{c}{{a + b}} = {\tan ^{ - 1}}(1)which gives us the required answer.

Complete step by step answer:
Consider△ABC\vartriangle ABC, where∠A=90∘\angle A = 90^\circ . Therefore, B+C=90∘B + C = {90^ \circ }

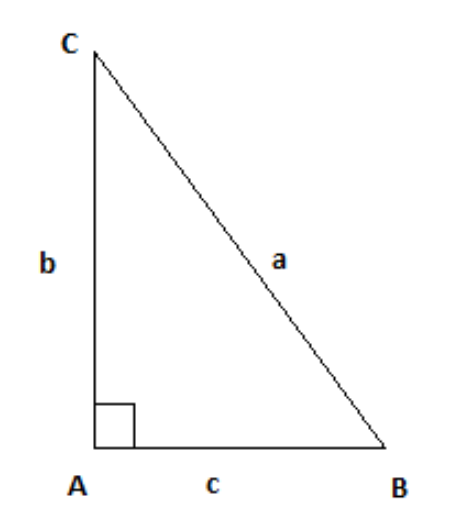
Let,
a = length of side BC
b = length of side AC
c = length of side AB
Since∠A=90∘\angle A = 90^\circ , we can use the Pythagoras’ theorem.
According to the Pythagoras’ theorem, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides of the right angled triangle where hypotenuse is the side opposite to the right angle.
Therefore, we havea2=b2+c2..........(1){a^2} = {b^2} + {c^2}..........(1)
We will use the inverse trigonometric formulatan⁡−1x+tan⁡−1y=tan⁡−1(x+y1−xy){\tan ^{ - 1}}x + {\tan ^{ - 1}}y = {\tan ^{ - 1}}(\dfrac{{x + y}}{{1 - xy}})to compute the value oftan⁡−1ba+c+tan⁡−1ca+b{\tan ^{ - 1}}\dfrac{b}{{a + c}} + {\tan ^{ - 1}}\dfrac{c}{{a + b}}.
Letx=ba+cx = \dfrac{b}{{a + c}}andy=ca+by = \dfrac{c}{{a + b}}.
Then after substituting the values ofxxandyy, we get
tan⁡−1ba+c+tan⁡−1ca+b =tan⁡−1(ba+c+ca+b1−(ba+c)(ca+b)) =tan⁡−1(ba+c+ca+b1−(ba+c)(ca+b)) =tan⁡−1(b(a+b)+c(a+c)(a+c)(a+b)1−(bc(a+c)(a+b))) =tan⁡−1(b(a+b)+c(a+c)(a+c)(a+b)((a+c)(a+b)−bc(a+c)(a+b)))  {\tan ^{ - 1}}\dfrac{b}{{a + c}} + {\tan ^{ - 1}}\dfrac{c}{{a + b}} \\\ = {\tan ^{ - 1}}(\dfrac{{\dfrac{b}{{a + c}} + \dfrac{c}{{a + b}}}}{{1 - (\dfrac{b}{{a + c}})(\dfrac{c}{{a + b}})}}) \\\ = {\tan ^{ - 1}}(\dfrac{{\dfrac{b}{{a + c}} + \dfrac{c}{{a + b}}}}{{1 - (\dfrac{b}{{a + c}})(\dfrac{c}{{a + b}})}}) \\\ = {\tan ^{ - 1}}(\dfrac{{\dfrac{{b(a + b) + c(a + c)}}{{(a + c)(a + b)}}}}{{1 - (\dfrac{{bc}}{{(a + c)(a + b)}})}}) \\\ = {\tan ^{ - 1}}(\dfrac{{\dfrac{{b(a + b) + c(a + c)}}{{(a + c)(a + b)}}}}{{(\dfrac{{(a + c)(a + b) - bc}}{{(a + c)(a + b)}})}}) \\\
We have fractions in the numerator and the denominator. Moreover, these fractions have the same denominator.
Therefore, we can cancel these common denominators out in order to simplify our expression further.
Now, we are left with
tan⁡−1ba+c+tan⁡−1ca+b =tan⁡−1(b(a+b)+c(a+c)(a+c)(a+b)−bc)  {\tan ^{ - 1}}\dfrac{b}{{a + c}} + {\tan ^{ - 1}}\dfrac{c}{{a + b}} \\\ = {\tan ^{ - 1}}(\dfrac{{b(a + b) + c(a + c)}}{{(a + c)(a + b) - bc}}) \\\
We can now apply the identity(x+a)(x+b)=x2+(a+b)x+ab(x + a)(x + b) = {x^2} + (a + b)x + abin the denominator.
tan⁡−1ba+c+tan⁡−1ca+b =tan⁡−1(ba+b2+ca+c2)a2+(c+b)a+cb−bc) =tan⁡−1(ba+b2+ca+c2)a2+ca+ba+cb−bc) =tan⁡−1(ba+b2+ca+c2)a2+ca+ba)  {\tan ^{ - 1}}\dfrac{b}{{a + c}} + {\tan ^{ - 1}}\dfrac{c}{{a + b}} \\\ = {\tan ^{ - 1}}(\dfrac{{ba + {b^2} + ca + {c^2})}}{{{a^2} + (c + b)a + cb - bc}}) \\\ = {\tan ^{ - 1}}(\dfrac{{ba + {b^2} + ca + {c^2})}}{{{a^2} + ca + ba + cb - bc}}) \\\ = {\tan ^{ - 1}}(\dfrac{{ba + {b^2} + ca + {c^2})}}{{{a^2} + ca + ba}}) \\\
We can use equation(1)(1)in the numerator of the above expression. It can be seen that the numerator becomes equal to the denominator after the substitution.
tan⁡−1ba+c+tan⁡−1ca+b =tan⁡−1(ba+a2+ca)a2+ca+ba)  {\tan ^{ - 1}}\dfrac{b}{{a + c}} + {\tan ^{ - 1}}\dfrac{c}{{a + b}} \\\ = {\tan ^{ - 1}}(\dfrac{{ba + {a^2} + ca)}}{{{a^2} + ca + ba}}) \\\
a, b, and c are the lengths of the sides of triangle ABC and hence each of them is a positive real number. Therefore, the denominator contains a non-zero real number.
This implies that we can divide the numerator by the denominator to obtain 1 as follows:
tan⁡−1ba+c+tan⁡−1ca+b =tan⁡−1(1)  {\tan ^{ - 1}}\dfrac{b}{{a + c}} + {\tan ^{ - 1}}\dfrac{c}{{a + b}} \\\ = {\tan ^{ - 1}}(1) \\\
Sincetan⁡−1(1)=π4{\tan ^{ - 1}}(1) = \dfrac{\pi }{4}, we gettan⁡−1ba+c+tan⁡−1ca+b=π4{\tan ^{ - 1}}\dfrac{b}{{a + c}} + {\tan ^{ - 1}}\dfrac{c}{{a + b}} = \dfrac{\pi }{4}
Hence the required answer isπ4\dfrac{\pi }{4}.

Note: We can use the formula tan⁡−1x+tan⁡−1y=tan⁡−1(x+y1−xy){\tan ^{ - 1}}x + {\tan ^{ - 1}}y = {\tan ^{ - 1}}(\dfrac{{x + y}}{{1 - xy}})to solve such a problem only if xy < 1.
This condition holds true for the above problem because a, b, and c are lengths of sides and the sum of the lengths of two sides is always greater than the third side. Therefore, x=ba+cx = \dfrac{b}{{a + c}}andy=ca+by = \dfrac{c}{{a + b}}both have numerator < denominator. Thus, we can see x, y < 1 and so is their product.