Question

In variable conservative potential energy field in a confined space, an electron has total mechanical energy of E₀. The potential energy is $-\frac{E_0}{2}$ for half the space and $\frac{E_0}{2}$ for the remaining half. Find ratio of largest de Broglie wavelength to smallest one for electron in given space

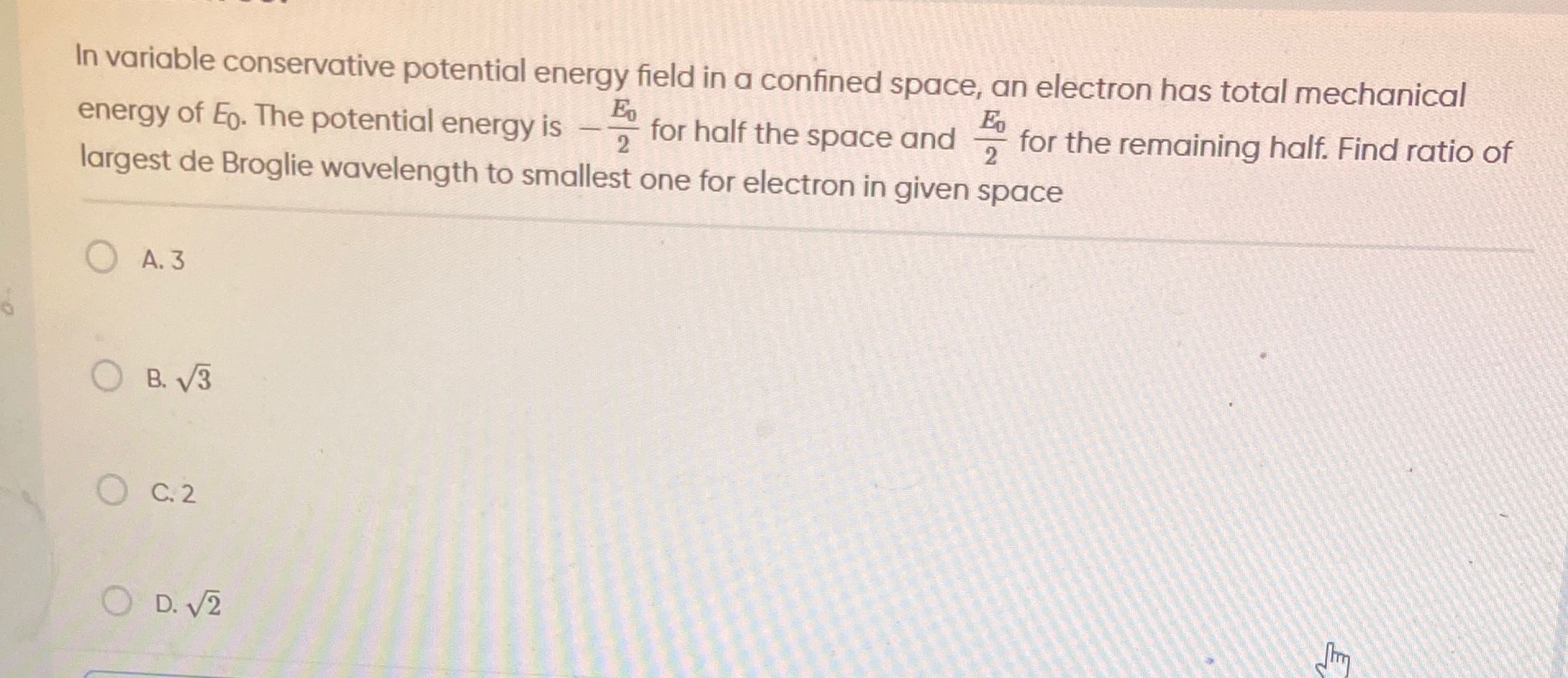
• A. 3
• B. √3
• C. 2
• D. √2

Answer 1

Answer: (B)

$\sqrt{3}$

Answer 2

The de Broglie wavelength $\lambda$ is related to the momentum $p$ of a particle by $\lambda = \frac{h}{p}$. The kinetic energy $K$ is related to momentum by $K = \frac{p^2}{2m}$, which implies $p = \sqrt{2mK}$. Substituting this into the de Broglie wavelength formula gives $\lambda = \frac{h}{\sqrt{2mK}}$. This shows that the de Broglie wavelength is inversely proportional to the square root of the kinetic energy ($\lambda \propto \frac{1}{\sqrt{K}}$). Therefore, the largest wavelength corresponds to the smallest kinetic energy, and the smallest wavelength corresponds to the largest kinetic energy.

The total mechanical energy $E$ of the electron is given as $E_0$. The kinetic energy $K$ in any region is given by $K = E_0 - U$, where $U$ is the potential energy in that region. For the electron to exist in a region, its kinetic energy must be non-negative ($K \ge 0$), which implies $E_0 \ge U$.

Region 1: Potential Energy, $U_1 = -\frac{E_0}{2}$. Kinetic Energy, $K_1 = E_0 - U_1 = E_0 - (-\frac{E_0}{2}) = E_0 + \frac{E_0}{2} = \frac{3E_0}{2}$. For $K_1 \ge 0$, we must have $E_0 \ge 0$.

Region 2: Potential Energy, $U_2 = \frac{E_0}{2}$. Kinetic Energy, $K_2 = E_0 - U_2 = E_0 - \frac{E_0}{2} = \frac{E_0}{2}$. For $K_2 \ge 0$, we must have $E_0 \ge 0$.

Assuming $E_0 > 0$ (as $E_0=0$ would lead to infinite wavelengths, and negative $E_0$ would lead to negative kinetic energy), we compare the kinetic energies: $K_1 = \frac{3E_0}{2}$ $K_2 = \frac{E_0}{2}$

Clearly, $K_2 < K_1$. Thus, the smallest kinetic energy is $K_{min} = K_2 = \frac{E_0}{2}$, and the largest kinetic energy is $K_{max} = K_1 = \frac{3E_0}{2}$.

The largest de Broglie wavelength ($\lambda_{largest}$) will occur where kinetic energy is smallest ($K_2$), and the smallest de Broglie wavelength ($\lambda_{smallest}$) will occur where kinetic energy is largest ($K_1$). So, $\lambda_{largest} \propto \frac{1}{\sqrt{K_2}}$ and $\lambda_{smallest} \propto \frac{1}{\sqrt{K_1}}$.

The ratio of the largest de Broglie wavelength to the smallest one is: $\frac{\lambda_{largest}}{\lambda_{smallest}} = \frac{1/\sqrt{K_2}}{1/\sqrt{K_1}} = \sqrt{\frac{K_1}{K_2}}$ Substituting the values of $K_1$ and $K_2$: $\frac{\lambda_{largest}}{\lambda_{smallest}} = \sqrt{\frac{3E_0/2}{E_0/2}} = \sqrt{\frac{3}{1}} = \sqrt{3}$

The ratio of the largest de Broglie wavelength to the smallest one is $\sqrt{3}$.