Question
Question: In $\triangle ABC$, with usual notations, if $a, b, c$ are in A. P. Then $a \cos^2 (\frac{C}{2}) + c...
In △ABC, with usual notations, if a,b,c are in A. P. Then acos2(2C)+ccos2(2A)=
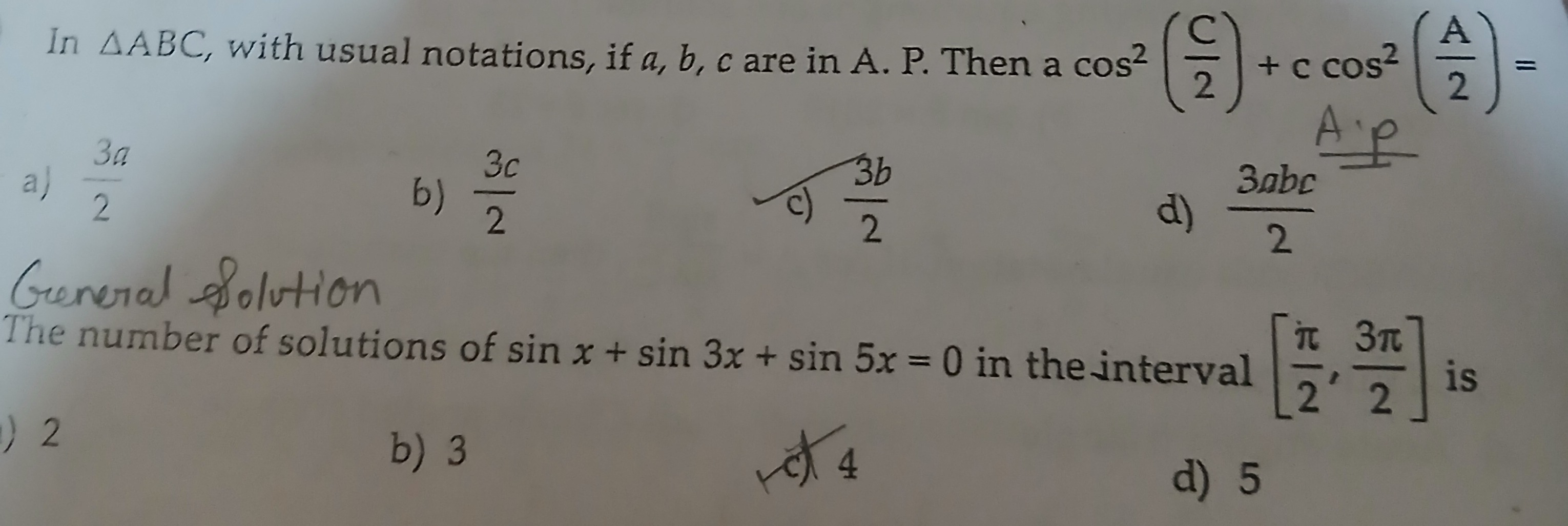
A
23a
B
23c
C
23b
D
23abc
Answer
23b
Explanation
Solution
-
Use the Half-Angle Formula:
In any triangle, one useful formula is:
cos2(2A)=bcs(s−a),cos2(2C)=abs(s−c),
where s=2a+b+c is the semiperimeter.
-
Substitute into the Expression:
acos2(2C)+ccos2(2A)=aabs(s−c)+cbcs(s−a)
This simplifies to:
bs(s−c)+bs(s−a)=bs[(s−c)+(s−a)].
Notice that
(s−c)+(s−a)=2s−(a+c).
Since s=2a+b+c, we have:
2s=a+b+cso2s−(a+c)=b.
Therefore,
acos2(2C)+ccos2(2A)=bs⋅b=s.
-
Use the A.P. Condition:
Since a, b, c are in A.P., we have:
b=2a+c⇒a+b+c=(a+c)+b=2b+b=3b.
Hence,
s=2a+b+c=23b.
Therefore, acos2(2C)+ccos2(2A)=23b.
