Question
Question: In triangle \[ABC\], right-angled at \[B\], \[AB = 24{\text{ cm}}\] and \[BC = 7{\text{ cm}}\]. Dete...
In triangle ABC, right-angled at B, AB=24 cm and BC=7 cm. Determine
(i) sinA, cosA
(ii) sinC, cosC
Solution
Here, we need to find the value of the sine and cosine of angles A and C. First, we will find the length of the hypotenuse using the Pythagoras’s theorem. Then, using the lengths of the sides of the right angled triangle, we can find the required trigonometric ratios using the formulae sinθ=HypotenusePerpendicular and cosθ=HypotenuseBase.
Formula Used: We will use the following formula to solve the question:
1.The Pythagoras’s theorem states that the square of the hypotenuse of a right angled triangle is equal to the sum of squares of the other two sides.
2.The sine of an angle θ of a right angled triangle is given by sinθ=HypotenusePerpendicular.
3.The cosine of an angle θ of a right angled triangle is given by cosθ=HypotenuseBase.
Complete step-by-step answer:
(i)
First, we will draw the diagram using the given information.
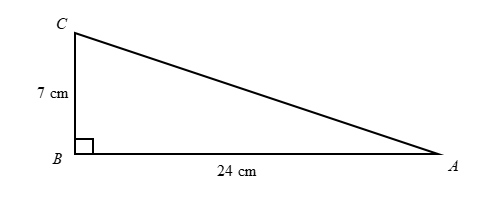
Here, ∠B=90∘, AB=24 cm and BC=7 cm.
We know that the side opposite to the right angle of a right angled triangle is the hypotenuse.
Therefore, AC is the hypotenuse.
Now, we will use the Pythagoras’s theorem to get the length of the hypotenuse.
The Pythagoras’s theorem states that the square of the hypotenuse of a right angled triangle is equal to the sum of squares of the other two sides, that is Hypotenusee2=Base2+Perpendicularr2.
Therefore, in triangle ABC, we get
AC2=AB2+BC2
Substituting AB=24 cm and BC=7 cm in the equation, we get
⇒AC2=242+72
Applying the exponents on the bases, we get
⇒AC2=576+49
Adding 576 and 49, we get
⇒AC2=625
Taking the square root of both sides, we get
