Question

In triangle ABC, right-angled at A, if $\tan C=\sqrt{3}$, find the value of sin B cos C + cos B sin C.

Answer 1

First of all, consider a triangle ABC and AB as $\sqrt{3}x$ and AC as x. Now find BC by using Pythagoras theorem. Now, find sin B and sin C by using $\sin \theta =\dfrac{Perpendicular}{Hypotenuse}$ and find cos C by using $\cos \theta =\dfrac{Base}{Hypotenuse}$ by substituting these values in the given expression to get the required answer.

Complete step-by-step answer:
Here, we are given a triangle ABC, right-angled at A. We are also given that $\tan C=\sqrt{3}$, we have to find the value of sin B cos C + cos B sin C. Let us consider a triangle ABC, right-angled at A.

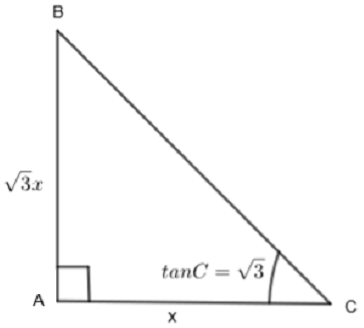
Here, we are given that $\tan C=\sqrt{3}$. We know that,
$\tan \theta =\dfrac{Perpendicular}{Base}$
We can see that, with respect to angle C,
Perpendicular = AB
Base = AC
We are given that
$\tan C=\dfrac{\sqrt{3}}{1}=\dfrac{AB}{AC}$
So, let us consider AB as $\sqrt{3}x$ and AC as x.
We know that Pythagoras theorem states that in a right-angled triangle, the square of the hypotenuse side is equal to the sum of the squares of the other two sides. So, in the above triangle ABC, by applying Pythagoras theorem, we get,
${{\left( AB \right)}^{2}}+{{\left( AC \right)}^{2}}={{\left( BC \right)}^{2}}$
Now by substituting the value of AB = $\sqrt{3}x$ and AC = x, we get,
${{\left( \sqrt{3}x \right)}^{2}}+{{\left( x \right)}^{2}}={{\left( BC \right)}^{2}}$
$3{{x}^{2}}+{{x}^{2}}=B{{C}^{2}}$
$B{{C}^{2}}=4{{x}^{2}}$
$BC=\sqrt{4{{x}^{2}}}$
$BC=2x$

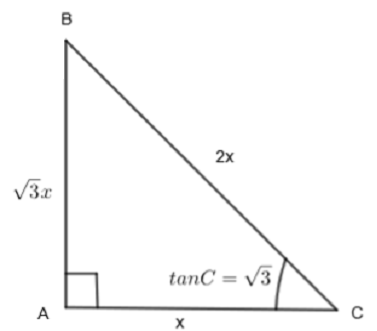
Now, with respect to angle C,
Perpendicular = AB = $\sqrt{3}x$
Base = AC = x
Hypotenuse = BC = 2x
We know that,
$\sin C=\dfrac{Perpendicular}{Hypotenuse}=\dfrac{AB}{BC}$
So, we get,
$\sin C=\dfrac{\sqrt{3}x}{2x}=\dfrac{\sqrt{3}}{2}....\left( i \right)$
We also know that,
$\cos C=\dfrac{Base}{Hypotenuse}=\dfrac{AC}{BC}$
So, we get,
$\cos C=\dfrac{x}{2x}=\dfrac{1}{2}....\left( ii \right)$
Now, with respect to angle B,
Perpendicular = AC = x
Base = AB = $\sqrt{3}x$
Hypotenuse = BC = 2x
We know that,
$\sin B=\dfrac{P}{H}=\dfrac{AC}{BC}$
So, we get,
$\sin B=\dfrac{x}{2x}=\dfrac{1}{2}....\left( iii \right)$
We also know that,
$\cos B=\dfrac{Base}{Hypotenuse}=\dfrac{AB}{BC}$
So, we get,
$\cos B=\dfrac{\sqrt{3}x}{2x}=\dfrac{\sqrt{3}}{2}...\left( iv \right)$
Now, let us consider the expression given in the question.
E = sin B cos C + cos B sin C
Now by substituting the values of sin B, sin C, cos B and cos C in the above expression, we get,
$E=\left( \dfrac{1}{2} \right)\left( \dfrac{1}{2} \right)+\left( \dfrac{\sqrt{3}}{2} \right)\left( \dfrac{\sqrt{3}}{2} \right)$
$E=\dfrac{1}{4}+\dfrac{3}{4}$
$E=\dfrac{4}{4}=1$
Here, we get the value of sin B cos C + cos B sin C as 1.

Note: Students can also do this question by considering the trigonometric table for general angles in the following way.
We know that,
$\tan {{60}^{o}}=\tan C=\sqrt{3}$
So, we get,
$\angle C={{60}^{o}}$
We already know that,
$\angle A={{90}^{o}}$
In a triangle,
$\angle A+\angle B+\angle C={{180}^{o}}$
So, we get,
$\angle B={{30}^{o}}$
We know that,
$\sin B\cos C+\cos B\sin C=\sin \left( B+C \right)=\sin \left( {{30}^{o}}+{{60}^{o}} \right)=\sin {{90}^{o}}$
We know that,
$\sin {{90}^{o}}=1$
So, we get, sin B cos C + cos B sin C = 1