Question

In triangle ABC, ‘D’ and ‘E’ are two points on sides AB and AC, respectively such that DE is parallel to BC. If AD=16 cm, BD=(5x-16) cm, AE=2x cm and EC=(25-2x) cm, then find the value of ‘x’.

• A. $2\sqrt10$
• B. $3\sqrt5$
• C. $4\sqrt5$
• D. $3\sqrt10$

Answer 1

Answer: (A)

$2\sqrt10$

Answer 2

The correct option is (A): $2\sqrt10$.

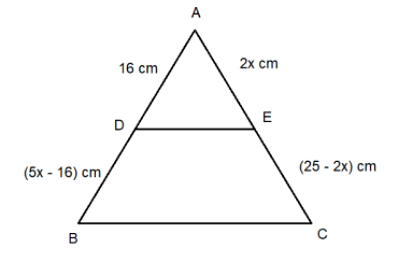
In triangle ABC, DE is parallel to BC
Therefore, triangle ADE is similar to triangle ABC
Therefore,
$(\frac{AD}{AB}) = (\frac{AE}{AC})$
Or, {$\frac{16}{(5x – 16 + 16)}$} = {$\frac{2x}{(25 – 2x + 2x)}$}
Or, 5x × 2x = 16 × 25
Or, 10x2 = 400
Or, x2 = 40
Or, x = $2\sqrt{10}$ (Since, length cannot be negative).