Question

In triangle $ABC,\angle A = \dfrac{\pi }{3}$ and it’s encircle is of units radius. If the radius of the circle touching the sides $AB,AC$ internally and encircle externally is x, then the value of x is
(A) $\dfrac{1}{2}$
(B) $\dfrac{1}{4}$
(C) $\dfrac{1}{3}$
(D) None of these

Answer 1

First, we have to draw a circle with the given conditions. Then we compare the sides and angles for some similarity using trigonometric values and solve for $x$and $y$. An acute angle is extensively used in this solution.

Complete answer:
First, we draw a circle with a unit radius.

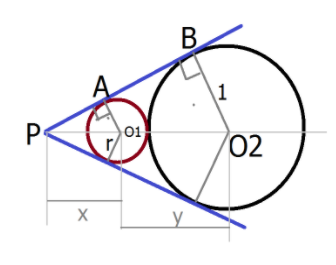
Secondly, we mark the radius as 1 with center $o2$
Forming a triangle ABC we see that the circle with unit radius touches the circle at abs and AC
Again we draw an encircle with radius x with center $o1$
Hence we get the above diagram
From the above diagram we get right-angled triangles $APO1$ AND $ABO2$
Hence we can write it as
$(x + y)\sin (30) = 1$
We write $\sin (30)$because the angle formed is $\sin (30)$
Hence we know that $\sin 30 = \dfrac{1}{2}$
Substituting the values we get,
$(x + y)\sin 30 = 1$
$(x + y)\dfrac{1}{2} = 1$
$x + y = 2$
Again we know that
$x\sin 30 = r$
Because the angle formed by the encircling has a radius $r$
Therefore we have:
$x = 2r$
Again for $y = 1 + r$
Solving this we get
$x + y = 2$
$2r + 1 + r = 2$
$3r + 1 = 2$
$3r = 2 - 1$
$3r = 1$
$r = \dfrac{1}{3}$

Hence the correct option is (C) i.e. $\dfrac{1}{3}$

Additional information:
Triangles and their properties are an essential part of solving questions as such. The trigonometric application adds to the sum to give the final answer.

Note:
Geometry and construction of triangles should be clear along with a clear understanding of their properties and formulas. Trigonometric formula i.e. $\sin (30)$is an essential part to proceed as it forms an angle with the triangle. The knowledge of adjacent sides along with values of trigonometric is essential.