Question

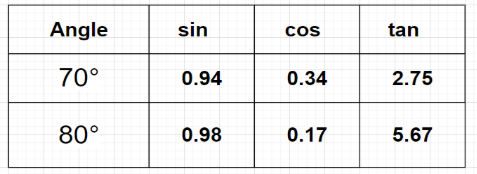
In triangle ABC, AB=5 cm, $\angle {\text{A}} = {80^0}$ and $\angle {\text{B}} = {70^0}$. Calculate the radius of the circumcircle and length of the other two sides. (Necessary values can be taken from the following table)

Answer 1

Hint: Here, we will proceed by using the property of the triangle i.e., the sum of all the interior angles of any triangle is always ${180^0}$ and then we will use the formula of extended sine rule i.e., $\dfrac{{{\text{AB}}}}{{\sin {\text{C}}}} = \dfrac{{{\text{BC}}}}{{\sin {\text{A}}}} = \dfrac{{{\text{AC}}}}{{\sin {\text{B}}}} = 2{\text{R}}$.

Complete step-by-step answer:

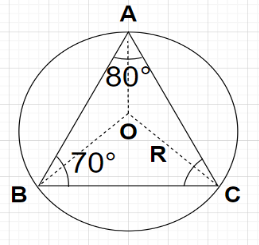
Given, in triangle ABC, AB=5 cm, $\angle {\text{A}} = {80^0}$ and $\angle {\text{B}} = {70^0}$
Let R cm be the radius of the circumcircle of the triangle ABC and O be the centre of this circumcircle.
i.e., OA=OB=OC=R cm
As we know that the sum of all the interior angles of any triangle is always ${180^0}$
For triangle ABC,
$\angle {\text{A}} + \angle {\text{B}} + \angle {\text{C}} = {180^0} \\\ \Rightarrow {80^0} + {70^0} + \angle {\text{C}} = {180^0} \\\ \Rightarrow \angle {\text{C}} = {180^0} - \left( {{{80}^0} + {{70}^0}} \right) \\\ \Rightarrow \angle {\text{C}} = {180^0} - {150^0} \\\ \Rightarrow \angle {\text{C}} = {30^0} \\\$
Also we know that according to the extended sine rule
$\dfrac{{{\text{AB}}}}{{\sin {\text{C}}}} = \dfrac{{{\text{BC}}}}{{\sin {\text{A}}}} = \dfrac{{{\text{AC}}}}{{\sin {\text{B}}}} = 2{\text{R }} \to {\text{(1)}}$
By substituting the known values, equation (1) becomes
$\dfrac{5}{{\sin {{30}^0}}} = \dfrac{{{\text{BC}}}}{{\sin {{80}^0}}} = \dfrac{{{\text{AC}}}}{{\sin {{70}^0}}} = 2{\text{R }} \to {\text{(2)}}$
According to the given table, $\sin {80^0} = 0.98$ and $\sin {70^0} = 0.94$
According to the general trigonometric table, $\sin {30^0} = 0.5$
Now, substitute the above values in equation (2), we get

$$\dfrac{5}{{0.5}} = \dfrac{{{\text{BC}}}}{{0.98}} = \dfrac{{{\text{AC}}}}{{0.94}} = 2{\text{R}} \\\ \Rightarrow 10 = \dfrac{{{\text{BC}}}}{{0.98}} = \dfrac{{{\text{AC}}}}{{0.94}} = 2{\text{R }} \to {\text{(3)}} \\\$$

By equation (3), we can write

$$10 = 2{\text{R}} \\\ \Rightarrow {\text{R}} = \dfrac{{10}}{2} \\\ \Rightarrow {\text{R}} = 5{\text{ cm}} \\\$$

So, the radius of the circumcircle of the triangle ABC is equal to 5 cm.
By equation (3), we can write

$$10 = \dfrac{{{\text{BC}}}}{{0.98}} \\\ \Rightarrow {\text{BC}} = 0.98 \times 10 \\\ \Rightarrow {\text{BC}} = 9.8{\text{ cm}} \\\$$

So, the length of side BC of the triangle ABC is equal to 9.8 cm.
By equation (3), we can write

$$10 = \dfrac{{{\text{AC}}}}{{0.94}} \\\ \Rightarrow {\text{AC}} = 10 \times 0.94 \\\ \Rightarrow {\text{AC}} = 9.4{\text{ cm}} \\\$$

So, the length of side AC of the triangle ABC is equal to 9.4 cm.

Note: In this particular problem, with the help of the given table we are only using the values of $\sin {80^0} = 0.98$ and $\sin {70^0} = 0.94$ whereas the other values are not used for the evaluation of the parameters asked. Here, we have used the extended sine rule because we know the values of all the interior angles and the length of one side.