Solveeit Logo
Login

Question

Question: In triangle ABC, \(A=31.4,B=53.7,\angle C={{61.3}^{\circ }}\),how do you find the area?...

In triangle ABC, A=31.4,B=53.7,∠C=61.3∘A=31.4,B=53.7,\angle C={{61.3}^{\circ }},how do you find the area?

Explanation

Solution

The question asks for the value of area of a triangle when the 2 sides and the third angle is given . Although the area of the triangle is defined as A=12×b×hA=\dfrac{1}{2}\times b\times h , where “b” is the base of the triangle , “h” is the height of the triangle. But if we don’t know the height of the given triangle, the formula used is A=12b(asin⁡C)A=\dfrac{1}{2}b(a\sin C) , where a , b are the sides of the triangle and ∠C\angle C is the third angle of the triangle.

Complete step by step solution:
Now consider a triangle ABC which is not a right-angled triangle , the 2 sides are a, b and third angle is C. If we make an perpendicular to the base BC naming the line to be AD then h becomes h=asin⁡Ch=a\sin C the on substituting the value of h in the formula then the area A changes to A=12b(asin⁡C)A=\dfrac{1}{2}b(a\sin C). Given two sides of a triangle a and b and the angle C between sides a and b (also called the inclusive angle ), the sine area formula is this formed .

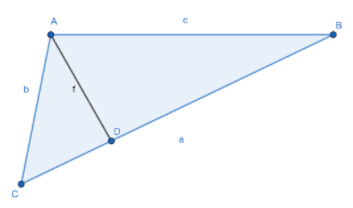
sin⁡C=ADAC=fb f=bsin⁡C Substituting in A=12base×height(h) ∴Area of triangle becomes  A=12absin⁡C \begin{aligned} & \sin C=\dfrac{AD}{AC}=\dfrac{f}{b} \\\ & f=b\sin C \\\ & \text{Substituting in A=}\dfrac{1}{2}base\times height(h) \\\ & \therefore \text{Area of triangle becomes } \\\ & A=\dfrac{1}{2}ab\sin C \\\ \end{aligned}
The values of the sides of the triangle are known to us and they are :
A=31.4,B=53.7,∠C=61.3∘A=31.4,B=53.7,\angle C={{61.3}^{\circ}}
The sin of angle C (∠C\angle C ) is:
sin⁡61.3∘=0.887\sin {{61.3}^{\circ}}=0.887
The area of a triangle is
A=12×A×B×sin⁡∠CA=\dfrac{1}{2}\times A\times B\times \sin \angle C
On putting the values of the respective variable , we get
⇒12×31.4×53.7×0.877 =739.38m2 \begin{aligned} & \Rightarrow \dfrac{1}{2}\times 31.4\times 53.7\times 0.877 \\\ & =739.38{{m}^{2}} \\\ \end{aligned}
∴\therefore The area of the triangle is 739.38m2739.38{{m}^{2}}.

Note: The value of sine of an angle will always be less than 1 . The formula given above can be applied to any type of triangle being acute , obtuse , right angle for finding the area of the triangle. This works when 2 sides and the third angle of a triangle are given.