Question

In trapezium PQRS, given that $QR\parallel PS$ and $2QR = PS$ . If $\overrightarrow {PQ} = \overrightarrow a$ , $\overrightarrow {QR} = \overrightarrow b$ and $\overrightarrow {RS} = \overrightarrow c$ , express $\overrightarrow a$ in terms $\overrightarrow b$ and $\overrightarrow c$ .

Answer 1

Hint : A quantity that has both magnitude and direction is called a vector quantity. A vector is either written in bold or is represented by an arrow above it. All the sides of the given trapezium represent a vector, from the relation between PS and QR, we can find the $\overrightarrow {PS}$ .

Complete step-by-step answer :

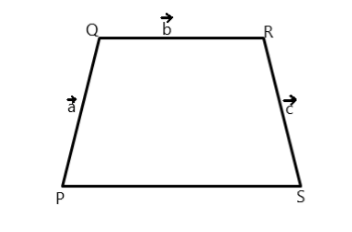
The direction of $\overrightarrow a$ is from P to Q, $\overrightarrow b$ is from Q to R, $\overrightarrow c$ is from R to S and the direction of $2\overrightarrow b$ is from P to S. That is when we start from P and take one revolution around PQRS, we see that the vector $\overrightarrow b$ starts from the head of the $\overrightarrow a$ , the $\overrightarrow c$ starts from the head of the $\overrightarrow b$ but the $2\overrightarrow b$ starts from the foot of $\overrightarrow a$ and ends at the head of the $\overrightarrow c$ . Thus $2\overrightarrow b$ is the only vector that is in the opposite direction while completing the revolution that’s why it is taken as negative while expressing the sum of all vectors in the closed trapezium PQRS.
We are given that $QR\parallel PS$ and $2QR = PS$ , so $PS = 2\overrightarrow b$
Now, the sum of all the vectors in a closed figure is equal to zero, so –
$\overrightarrow a + \overrightarrow b + \overrightarrow c + \overrightarrow {( - 2b} ) = 0 \\\ \overrightarrow b = \overrightarrow a + \overrightarrow c \\\ \Rightarrow \overrightarrow a = \overrightarrow b - \overrightarrow c \;$
So, the correct answer is “ $\overrightarrow a = \overrightarrow b - \overrightarrow c \;$ ”.

Note : If a closed polygon is formed by the set of vectors in a given order then the resultant vector is a null vector or zero vector. Using this information, we can find out the correct answer.