Question
Question: In trapezium ABCD, \[M \in \overline {AD} ,N \in \overline {BC} \] are the points such \[\dfrac{{AM}...
In trapezium ABCD, M∈AD,N∈BC are the points such MDAM=NCBN=32. The diagonal AC intersects MN atO. Then find the value of ACAO.
Solution
Hint: A trapezium is a 2D shape which falls under the category of quadrilaterals. A trapezium has two parallel sides and two non-parallel sides. Using this information first draw the diagram with the given data and solve the problem accordingly.
Complete step-by-step answer:
In the given trapezium ABCD, AB∥CD, M and Nare the points on the traversals AD and BC respectively as shown in the below diagram.
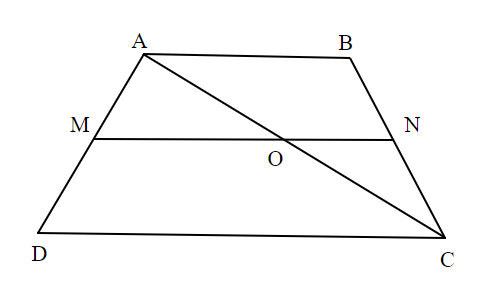
Also, given MDAM=NCBN=32
So, clearly from the diagram, MN∥AB and AB∥CD.
Given that diagonal AC intersects MN at O.
In ΔADC, MO∥DC such that M∈AD & O∈AC.
We know that by the Triangle Proportionality theorem, if a line parallel to one side of a triangle intersects the other two sides of the triangle, then the lines divide these two sides proportionally.
By using this property in ΔADC, we have
⇒MDAM=OCAO
But we have MDAM=32
So, OCAO=32
We have to find ACAO. From the diagram, OC=AO+OC
Thus, OCAO=52.
Note: The length of the mid-segment is equal to half of the sum of parallel bases in a trapezium. In this problem we have used both the properties of triangles as well as the properties of trapezium.
