Question

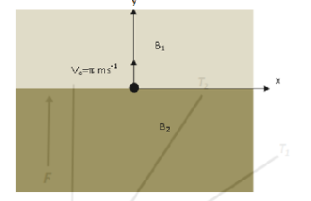
In the x-y plane, the region $y > 0$ has a uniform magnetic field ${B_1}\widehat {\text{k}}$ and the region $y < 0$ has another uniform magnetic field ${B_2}\widehat {\text{k}}$. A positively charged particle is projected from the origin along the positive y-axis with speed ${V_o} = \pi \,{\text{m}}{{\text{s}}^{{\text{ - 1}}}}$ at $t = 0$, as shown in the figure. Neglect gravity in this problem. Let $t = T$ be the time when the particle crosses the x-axis from below for the first time. If ${B_2} = 4{B_1}$, the average speed of the particle, in ${\text{m}}{{\text{s}}^{{\text{ - 1}}}}$, along the x-axis in the time interval $T$ is _________.

Answer 1

We are asked to find the average speed. For this we need to check the path that the charged particle will follow in a uniform magnetic field. Find the total distance travelled by the particle and the total time taken. Using these two values find the average speed of the particle.

Complete step by step solution:
Given, for the region $y > 0$, the magnetic field is ${B_1}\widehat {\text{k}}$
For the region $y < 0$, the magnetic field is ${B_2}\widehat {\text{k}}$
The velocity of the charged particle is ${V_o} = \pi \,{\text{m}}{{\text{s}}^{{\text{ - 1}}}}$ at $t = 0$.
The particle crosses the x-axis at $t = T$
And ${B_2} = 4{B_1}$.
The particle is said to be positively charged, let the charge of the particle be $q$
Let the mass of the charged particle be $m$
Here, the particle starts from origin and moves towards the positive y-axis also, a uniform magnetic field exists along the z-axis. When a charged particle motion is kept in a uniform magnetic field and direction of motion of the particle is perpendicular to the direction of magnetic field, then the charged particle experiences a force due to which the charged particle follows a curved path. The radius of this curved path is given by,
$r = \dfrac{{mv}}{{qB}}$ ……………..(i)

where $m$ is the mass of the charged particle, $v$ is the velocity of the charged particle, $B$ is the magnetic field strength and $q$ is the charge of the particle.
The time period of this circular motion is given by,
$T = \dfrac{{2\pi m}}{{qB}}$ ………………...(ii)
Since here, the motion of the charged particle is perpendicular to the direction of magnetic field, so the charged particles will follow a circular path in both $y > 0$ region and $y < 0$ region.
Let $R$ be the radius of the circular path for region $y > 0$ and $r$ be the radius of the circular path for region $y < 0$.
Let us draw a diagram for proper understanding.

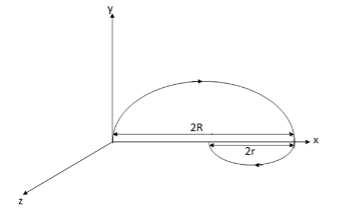
The radius $r$ is less than $R$, as from equation (i), we observe the larger the magnetic field, the smaller is the radius.
Now, using the formula from equation (i), we get the radius $R$ for region $y > 0$.
$R = \dfrac{{m{V_0}}}{{q{B_1}}}$ ………………...(iii)
The radius $r$ for region $y < 0$, using the formula from equation (i) is
$r = \dfrac{{m{V_0}}}{{q{B_2}}}$ ……………….(iv)
We have ${B_2} = 4{B_1}$, substituting this value in equation (iv) we get
$r = \dfrac{{m{V_0}}}{{4q{B_1}}}$ ……………….(v)
Now, from the figure, we observe that the total distance travelled by the particle is
$S = 2R + 2r$
Putting the values from equations (iii) and (v) in the above equation we get
$S = 2\left( {\dfrac{{m{V_0}}}{{q{B_1}}}} \right) + 2\left( {\dfrac{{m{V_0}}}{{4q{B_1}}}} \right)$
$\Rightarrow S = \dfrac{{2m{V_0}}}{{q{B_1}}} + \dfrac{{m{V_0}}}{{2q{B_1}}}$
$\Rightarrow S = \dfrac{{5m{V_0}}}{{2q{B_1}}}$
Now, the total time taken by the particle is addition of the time taken to complete the upper half circle and time taken to complete the lower half circle.
That is,
$T = {T_1} + {T_2}$ ……………...(vi)
where ${T_1}$ is the time period for the upper half circle and ${T_2}$ is the time period for the lower half circle.
We can write, from equation (ii)
${T_1} = \dfrac{1}{2} \times \dfrac{{2\pi m}}{{q{B_1}}}$ (half becomes its for half circle)
Similarly,
${T_2} = \dfrac{1}{2} \times \dfrac{{2\pi m}}{{q{B_2}}}$
Putting these values in equation (vi) and substituting ${B_2} = 4{B_1}$, we get
$T = \dfrac{1}{2} \times \dfrac{{2\pi m}}{{q{B_1}}} + \dfrac{1}{2} \times \dfrac{{2\pi m}}{{4q{B_1}}}$
$\Rightarrow T = \dfrac{{\pi m}}{{q{B_1}}} + \dfrac{{\pi m}}{{4q{B_1}}}$
$\Rightarrow T = \dfrac{{5\pi m}}{{4q{B_1}}}$
Now, average speed of the particle will be,
${V_{av}} = \dfrac{{{\text{Total distance travelled}}}}{{{\text{total time}}}}$
Here,
${V_{av}} = \dfrac{S}{T}$
Putting the values of $S$ and $T$, we get

\right)}}$$ $${V_{av}} = 2\,{\text{m}}{{\text{s}}^{{\text{ - 1}}}}$$ **Therefore, the average speed is $$2\,{\text{m}}{{\text{s}}^{{\text{ - 1}}}}$$.** **Note:** Always keep in mind that a charged particle in a uniform magnetic field will follow a curved path only when the motion of the particle and direction of magnetic field are perpendicular to each other, if they are parallel then the charged particle will not experience any magnetic force.