Question
Question: In the wheatstone’s network given, \(P = 10\Omega ,Q = 20\Omega ,R = 15\Omega ,S = 30\Omega ,\) the ...
In the wheatstone’s network given, P=10Ω,Q=20Ω,R=15Ω,S=30Ω, the current passing through the battery (of negligible internal resistance) is:
A. 0.36A
B. Zero
C. 0.18A
D0 0.72A
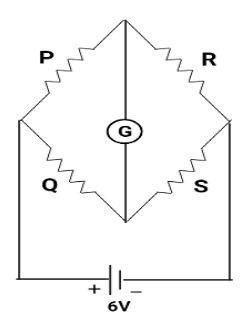
Solution
The Wheatstone bridge operates on the null deflection theorem, which states that their resistance ratios are identical and that no current passes through the circuit. In normal circumstances, the bridge is unbalanced, allowing current to pass through the galvanometer.
Complete step by step answer:
In the question it is given that,
P=10Ω ⇒Q=20Ω ⇒R=15Ω ⇒S=30Ω
Now , we see that
QP=2010=21
Similarly,
SR=3015=21
From the above two equations, We observe that QP=SR which states that their resistance ratios are identical. Hence, there is no current flowing through the galvanometer. Therefore, The Wheatstone bridge is satisfied.
Now, we see that P and R are in series. Hence, the net resistance will be,
R1=P+R ⇒R1=10Ω+15Ω ⇒R1=25Ω
Similarly, Q and S are also in series. Hence, the net resistance will be,
{R_2} = Q + S \\\
\Rightarrow {R_2} = 20\Omega + 30\Omega \\\
\Rightarrow {R_2} = 50\Omega \\\
Now, R1 and R2 are in parallel combination,
R1=R11+R21
⇒R1=501+251 ⇒R1=501+2 ⇒R1=503 ⇒R=350
Using ohm’s law, I=RV
We know that,
V=6V ⇒R=350Ω
Substituting these values we get,
I=RV ⇒I=506×3 ⇒I=5018 ∴I=0.36A
Hence, the correct answer is option A.
Note: A Wheatstone bridge is an electrical circuit that balances two legs of a bridge circuit, one of which contains the unknown part, to test an unknown electrical resistance. The circuit's main advantage is its ability to produce highly precise measurements.
