Question
Question: In the Wheatstone's bridge shown it current \[2A\] enters at A, then what is the value of current in...
In the Wheatstone's bridge shown it current 2A enters at A, then what is the value of current in arm BC?
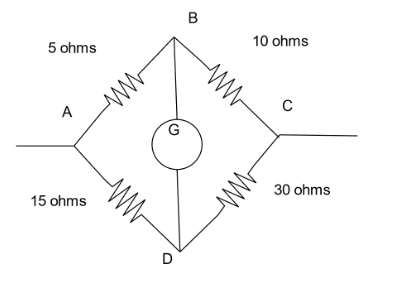
Solution
A Wheatstone bridge is an electrical circuit used to measure an unknown electrical resistance by adjusting two legs of an extension circuit, one leg of which incorporates the unknown segment. The essential advantage of the circuit is its capability to give amazingly accurate estimations
Formula used:
QP=SR
Where, P,Q,R and S are electrical resistances.
Ohm’s law: V=IR
Complete step by step answer:
It is given that a current of 2A is passing through the vertex A. Let the current flowing through the arm ABC be IAmperes.The current flowing through the arm ADC will be the remaining left from the value of 2A.The current flowing through the arm ADC be (2−I)Amperes.Since the voltage flowing through the circuit is unknown, we can take it as V.
The net resistance in arm ABC will be RABC=10+5=15
The net resistance in arm ADC will be RADC=30+15=45
We know that ohm’s law gives us the relation between current, resistance and voltage.
V=15I
⇒V=45(2−I)=90−45I
The voltage through arms ABC and ADC are the same, so we arrive at the equation:
Equating these two equations against each other, we have
