Question

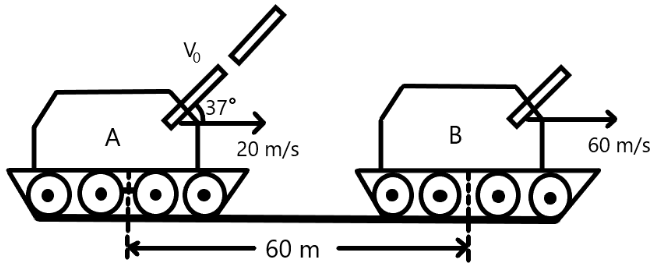
In the war zone, an army tank A is approaching the enemy tank B as shown in figure. A shell is fired from tank A with muzzle velocity ${v_0}$ at an angle $37^\circ$ to the horizontal at the instant when tank B is $60\,m$ away. Tank B which is moving away with velocity $60\,m{s^{ - 1}}$ is hit by shell, then ${v_0}$ is ($g = 10\,m{s^{ - 2}}$)

Answer 1

Here, the shell is fired from the tank A that strikes the tank B which is $60\,m$ away from the tank A. here, the shell is making a trajectory. Therefore, it will be taken as a projectile. Therefore, we will use the range of the projectile to calculate the velocity of the shell.

Complete step by step answer:
As given the question, a tank A is approaching the enemy tank B in the war zone. A shell is fired from tank A with velocity ${v_0}$ at an angle $37^\circ$ to the horizontal. This shell hits the tank B which is at a distance of $60\,m$ from the tank A. This shell will make a trajectory, therefore, we will consider the shell as projectile. Therefore, we will use the projectile motion formula to solve range and time period which is given below
Range $= \dfrac{{2{u_x}{u_y}}}{g}$
And time period $= \dfrac{{2{u_y}}}{g}$
Here, ${u_x}$ is the velocity of the tank A and ${u_y}$ is the velocity of the tank B.
Now, the horizontal velocity of the tank A is given by
${u_x} = {v_0}\cos 37^\circ + 20$
Now, the velocity of the tank B which is moving away with velocity $60\,m{s^{ - 1}}$ is given by
${u_y} = {v_0}\sin 37^\circ$
Therefore, the range of the tank A is given by
${R_A} = \dfrac{{2\left( {{v_0}\cos 37^\circ + 20} \right)\left( {{v_0}\sin 37^\circ } \right)}}{g}$
Also, the range of the tank is given by
${R_B} = \dfrac{{2\left( {{v_0}\sin 37^\circ } \right)}}{g} \times 60$
Now, for this situation, we will consider
${R_A} = 60 + {R_B}$
$\Rightarrow \,\dfrac{{2\left( {{v_0}\cos 37^\circ + 20} \right)\left( {{v_0}\sin 37^\circ } \right)}}{g} = 60 + \dfrac{{2\left( {{v_0}\sin 37^\circ } \right)}}{g} \times 60$
$\Rightarrow \,\dfrac{{2\left( {{v_0} \times \dfrac{4}{5} + 20} \right)\left( {{v_0}\dfrac{3}{5}} \right)}}{{10}} = 60 + \dfrac{{2\left( {{v_0}\dfrac{3}{5}} \right)}}{{10}} \times 60$
$\Rightarrow \,\dfrac{{2\left( {\dfrac{{4{v_0} + 100}}{5}} \right)\left( {\dfrac{{3{v_0}}}{5}} \right)}}{{10}} = 60 + \dfrac{{6{v_0}}}{{10 \times 5}} \times 60$
$\Rightarrow \,\dfrac{{3{v_0}\left( {8{v_0} + 200} \right)}}{{10 \times 25}} = 60 + \dfrac{{360{v_0}}}{{50}}$
$\Rightarrow \,\dfrac{{24v_0^2 + 600{v_0}}}{{250}} = \dfrac{{3000 + 360{v_0}}}{{50}}$
$\Rightarrow \,24v_0^2 + 600{v_0} = 5\left( {3000 + 360{v_0}} \right)$
$\Rightarrow \,24v_0^2 + 600{v_0} = 15000 + 1800{v_0}$
$\Rightarrow \,24v_0^2 - 1200{v_0} - 15000 = 0$
$\Rightarrow \,v_0^2 - 50{v_0} - 625 = 0$
Now, we will use the quadratic formula as shown below
${v_0} = \dfrac{{50 \pm \sqrt {2500 + 4 \times 625} }}{2}$
$\Rightarrow \,{v_0} = \dfrac{{50 \pm 50\sqrt 2 }}{2}$
$\therefore \,{v_0} = 25\left( {1 \pm \sqrt 2 } \right)m{s^{ - 1}}$
Therefore, the velocity shell fired from the tank A is $25\left( {1 \pm \sqrt 2 } \right)m{s^{ - 1}}$

Hence, option A is the correct option.

Note: Here, we have used the concept of projectile because the shell is making a trajectory. That is why, we have used the concept of the range to calculate the velocity of the shell. Also, we have added $60$ with the range of tank B because it is $60\,m$ away from the tank A.