Question
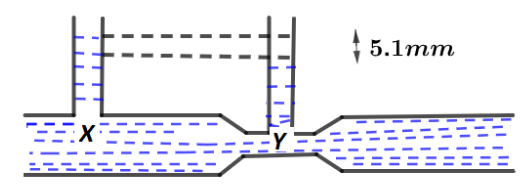
Question: In the venturimeter as shown, water is flowing. Speed at \(x\) is \(2\,cm\,{\sec ^{ - 1}}\). The Spe...
In the venturimeter as shown, water is flowing. Speed at x is 2cmsec−1. The Speed of water at y is ? (g=1000cmsec−2)
A. 23cmsec−1
B. 32cmsec−1
C. 101cmsec−1
D. 1024cmsec−1
Solution
In order to solve this question, we will use the definition of venturimeter. Venturimeter is a device that is used to measure the rate of flow of liquid through a pipe. This device is based on the principle of Bernoulli’s equation. It has three parts: Covering part, throat and Diverging part. Bernoulli’s principle depicts that when velocity increases pressure decreases. Water flows as there is pressure difference between inlet pipe and throat which can be measured using a differential manometer. After getting pressure difference flow rate is calculated
Complete step by step answer:
Given in question v1=2cmsec−1 where v1 is velocity of fluid at x
Similarly v2=vcmsec−1 , where v2 is velocity of fluid at y
And h=5.1mm=0.51cm
Using Bernoulli’s Principle at x and y we get
ρgp1+2gv12+z1=ρgp2+2gv22+z2
⇒ρgp1+2gv12=ρgp2+2gv22 since (z1=z2=0) As the tube is horizontal
⇒ρgp1−p2=2gv22−v12
⇒h=2gv22−v12 Where (h=ρgp1−p2) is the height difference between two water level at x & y
v22=v12+2gh
Putting values in above equation we get
v2=(2cmsec−1)2+(2×1000cmsec−2×0.51cm)
⇒v2=1024cm2sec−2
⇒v=32cmsec−1
Hence,The Speed of water at y is 32cmsec−1.
Note: It should be remembered that, continuity equation always valid at both x and y so flow would be continuous also in Bernoulli’s Principle we have put z1&z2 equal to zero because the venturimeter is horizontal in nature. It can be viewed that velocity at y is greater than velocity at x even pressure at y is less than pressure at x this clearly depicts the proof that Bernoulli's flow in the venturi meter could be laminar flow because of fluid continuity.
