Solveeit Logo
Login

Question

Question: In the venn diagram, the numbers represent the number of elements in the subsets. Given that \[\xi =...

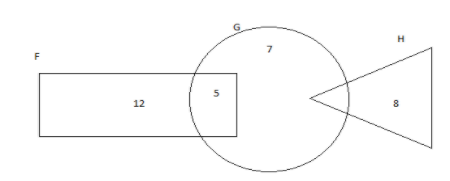
In the venn diagram, the numbers represent the number of elements in the subsets. Given that ξ=F∪G∪H\xi = F \cup G \cup H and n(ξ)=42,n\left( \xi \right) = 42, find n(G′∪H)n\left( {G' \cup H} \right) .

A.18
B.28
C.30
D.38

Explanation

Solution

Here, we have to find the cardinality of the given set. We will find the values of the cardinality from the Venn diagram and then by using the set formula, we will find the cardinality of the set. A set is defined as a collection of well-defined objects. Cardinality is defined as the number of elements in a set.

Formula Used:
We will use the following formula:
1.If we are given three finite set, then the total number is given by the formula n(U)=n(A)+n(B)+n(C)+n(A∩B)+n(B∩C)+n(A∩C)n\left( U \right) = n\left( A \right) + n\left( B \right) + n\left( C \right) + n\left( {A \cap B} \right) + n\left( {B \cap C} \right) + n\left( {A \cap C} \right)
2.n(G′∪H)=n(G′)+n(H)−n(G′∩H)n\left( {G' \cup H} \right) = n\left( {G'} \right) + n\left( H \right) - n\left( {G' \cap H} \right)

Complete step-by-step answer:
Let F, G, H represent the number of elements in the subsets respectively.
Number of elements in a subsets n(F)=12n\left( F \right) = 12
Number of elements in a subsets n(G)=7n\left( G \right) = 7
Number of elements in a subsets n(H)=8n\left( H \right) = 8
Number of elements in both the subsets n(F∩G)=5n\left( {F \cap G} \right) = 5
From the venn diagram, there are no common elements in the subsets F and H and there are no common elements in all the three subsets F, G, H.
We are also given that the total number of elements in the subset is 42.
If we are given three finite set, then the total number is given by the formula n(U)=n(A)+n(B)+n(C)+n(A∩B)+n(B∩C)+n(A∩C)n\left( U \right) = n\left( A \right) + n\left( B \right) + n\left( C \right) + n\left( {A \cap B} \right) + n\left( {B \cap C} \right) + n\left( {A \cap C} \right)
Now, substituting the terms in the above formula, we get
n(U)=n(F)+n(G)+n(H)+n(F∩G)+n(H∩G)+n(F∩H)n\left( U \right) = n\left( F \right) + n\left( G \right) + n\left( H \right) + n\left( {F \cap G} \right) + n\left( {H \cap G} \right) + n\left( {F \cap H} \right)
Substituting n(U)=42n\left( U \right) = 42, n(F)=12n\left( F \right) = 12,n(G)=7n\left( G \right) = 7, n(H)=8n\left( H \right) = 8 and n(F∩G)=5n\left( {F \cap G} \right) = 5 in the above equation, we get
⇒42=12+7+8+5+(H∩G)\Rightarrow 42 = 12 + 7 + 8 + 5 + \left( {H \cap G} \right)
Subtracting the like terms, we get
⇒n(G∩H)=42−12−7−8−5\Rightarrow n\left( {G \cap H} \right) = 42 - 12 - 7 - 8 - 5
⇒n(G∩H)=10\Rightarrow n\left( {G \cap H} \right) = 10
Now, we will find n(G′∪H)n\left( {G' \cup H} \right).
n(G′)=n(U)−n(G)n\left( {G'} \right) = n\left( U \right) - n\left( G \right)
⇒n(G′)=42−22=20\Rightarrow n\left( {G'} \right) = 42 - 22 = 20
We know that n(G∩H)=10n\left( {G \cap H} \right) = 10
n(H)=10+8=18n\left( H \right) = 10 + 8 = 18
Clearly n(G′∩H)=n(H)−n(G∩H)n\left( {G' \cap H} \right) = n\left( H \right) - n\left( {G \cap H} \right)
⇒n(G′∩H)=18−10=8\Rightarrow n\left( {G' \cap H} \right) = 18 - 10 = 8
⇒n(G′∪H)=n(G′)+n(H)−n(G′∩H)\Rightarrow n\left( {G' \cup H} \right) = n\left( {G'} \right) + n\left( H \right) - n\left( {G' \cap H} \right)
By substituting the values, we get
⇒n(G′∪H)=20+18−8\Rightarrow n\left( {G' \cup H} \right) = 20 + 18 - 8
⇒n(G′∪H)=30\Rightarrow n\left( {G' \cup H} \right) = 30
Therefore, n(G′∪H)n\left( {G' \cup H} \right) is 30.
Thus Option(C) is the correct answer.

Note: Venn diagram is a method to represent the relationships between the finite sets. A finite set is defined as the set which is countable. We should know that the universal set is defined as a set that contains all the elements of a set under consideration. We should know that the total members in the set is known as the universal set. The complement of a set (A′)\left( {A'} \right) is defined as the number of elements in the universal set but not in the set.