Question
Question: In the triangle above, the sine of \( x^\circ \) is 0.6. What is the cosine of \( y^\circ \) ? ...
In the triangle above, the sine of x∘ is 0.6. What is the cosine of y∘ ?
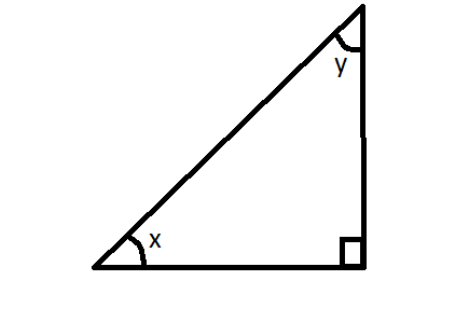
Solution
Hint : We know, sine and cosine are the ratios of side to the hypotenuse of a right angled triangle. So, to solve this problem, we have to find the sine of x∘ that resembles the ratio of which side to the hypotenuse of the triangle. Then we will find the cosine of y∘ resembles the ratio of which side to the hypotenuse. Then by using the value for sine of x∘ as given, we can find the required value, that is cosine of y∘ .
Complete step by step solution:
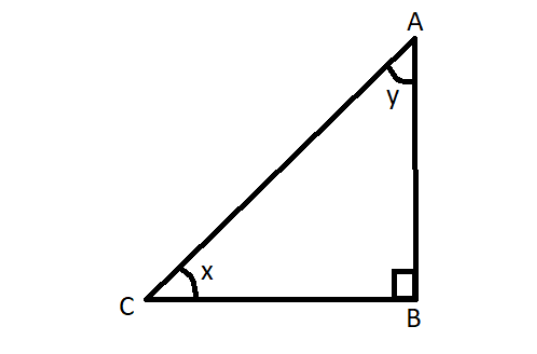
So, let us name the sides of the triangle as A,B,C , such that the right angle is at B .
The angle x∘ is at C and the angle y∘ is at A .
Now, we know, the sine of an angle is the ratio of the perpendicular to the hypotenuse in a right angled triangle.
Therefore, sine of x∘ can be written as, sinx=ACAB=0.6
Also, we know, cosine of an angle is the ratio of the base to the hypotenuse in a right angled triangle.
Therefore, we can write, cosine of y∘ as, cosy=ACAB
Therefore, it is clearly visible to us that, sinx=cosy=ACAB .
So, we get a cosine of y∘ as, cosy=ACAB=0.6 .
So, the correct answer is “0.6”.
Note : We can also solve this problem in another way that is, if the sine of an angle is 0.6=53 , then the angle is 37∘ , therefore, the other angle of the triangle other than right angle is clearly 53∘ . Therefore, the cosine of 53∘ is also 0.6=53 . The formulae of the trigonometric functions must be clearly understood before attempting such questions.
