Question
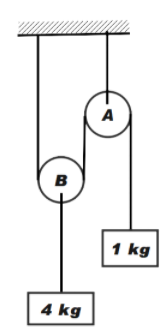
Question: In the system shown in the given figure, the acceleration of 1 kg mass is. ...
In the system shown in the given figure, the acceleration of 1 kg mass is.
A. 4gdownwards
B. 2gdownwards
C. 2gupwards
D. 4g upwards
Solution
In this question we have been asked to calculate the acceleration of the block of mass 1 kg. We know that for a pulley system the mass and acceleration can be calculated using the equation of motion. Therefore, we shall first draw the free body diagram of the given system and write the equation based on the diagram and thus calculate the answer.
Complete answer:
In the given diagram, we can see that the 4 kg block is connected with an entirely different string. Therefore, we shall relate the tension between the strings.
Consider the FBD of pulley A, as shown in the diagram below.
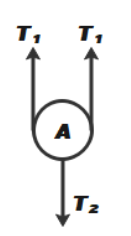
Now, from the above diagram we can say that,
2T1−T2=maaa
On solving,
2T1=T2
Let us consider the free body diagram for block system as shown below,
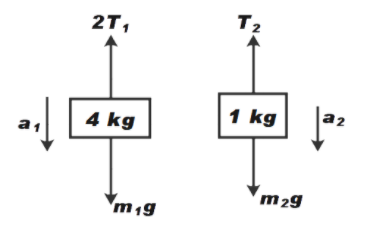
Now, to relate the strings we have constraint equation,
m2=−T2x2
m1=2T1x1
On solving,
We get,
2Tx1−Tx2=0
Therefore,
x2=2x1
Now, we know that differentiating twice the distance with respect to time we get acceleration
Therefore,
a2=2a1 ……………. (1)
Now, from the free body diagram
We get,
m2g−T=m2a2 ……………… (2)
Similarly,
2T−m1g=m1a1 …………… (3)
After substituting the values in equation (2) and (3)
We get,
g−T=2a1 …………….. (since a2=2a1)
2T−4g=4a1
On solving above equations simultaneously
We get,
−2g=−8a1
Therefore,
a1=4g……………….. (4)
Now from (1) and (4)
We get,
a2=−2g
The negative sign indicates that the acceleration of the block with 1 kg mass is upwards.
Therefore, the correct answer is option C.
Note:
The constraint equation is applied to find a relation between the motion of string i.e. the distance string moves due to acceleration on block. We know that work done by internal force is zero. If we consider the entire system as one unit, we get tension as the internal force. Therefore, using this concept the constraint equations are written.
