Question

In the system shown in the figure below, all the surfaces are smooth. If the value of $F$ is such that the block does not slide on the wedge, then the normal force acting on the block is

(A) $\dfrac{{\sqrt 3 }}{2}mg$
(B) $\sqrt 3 mg$
(C) $\dfrac{{mg}}{2}$
(D) $2mg$

Answer 1

Hint Since the surfaces are all smooth, the downward gravitational acceleration will be balanced by the external force only. Drawing a free body diagram will make force balance very easy to solve for the normal force.
Formula used: From the free body diagram, $F\cos \theta = mg\sin \theta$ and $N = mg\cos \theta + F \sin \theta$ . Here, $N$ is the normal force, $m$ is the mass of the block, $g = 9.8m/{s^2}$ is the gravitational acceleration and $\theta$ is the angle of the wedge with the horizontal.

Complete step by step answer
For such questions, we should always start by drawing a free body diagram of the system which is shown below:

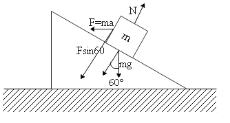
Since it has been given that the block of mass $m$ does not slide on the wedge, there is a pseudo force acting on it in the direction opposite to the actual force. Also, the forces acting on the block in the direction parallel to the wedge cancel each other out since the block doesn’t slide on the wedge.
So, we can write that:
$\Rightarrow ma\cos {60^ \circ } = mg\sin {60^ \circ }$
Dividing both sides by $m\cos \theta$ , we get
$\Rightarrow a = g\tan \theta$
The normal force is balanced by the pseudo force and the gravitational direction in the direction perpendicular to the surface of the wedge so we can write:
$\Rightarrow N = mg\cos {60^ \circ } + F\sin {60^ \circ }$
Substituting $F = ma$ , $\cos {60^ \circ } = 1/2$ and $\sin {60^ \circ } = \dfrac{{\sqrt 3 }}{2}$ , we get
$\Rightarrow N = \dfrac{{mg}}{2} + \dfrac{{\sqrt 3 }}{2}ma$
Further substituting $a = g\tan {60^ \circ } = \sqrt 3 g$ we get,
$\Rightarrow N = \dfrac{{mg}}{2} + \dfrac{{\sqrt 3 \left( {\sqrt 3 } \right)}}{2}mg \\\ = \dfrac{{mg}}{2} + \dfrac{3}{2}mg$
$\therefore N = 2mg$ which corresponds to option (D).
Hence, the correct option is option (D).

Note
While drawing the free body diagram, we must be careful while drawing the pseudo force acting on the block since it’ll have a direction opposite to the externally applied force. Further while calculating the normal force, we should also consider the component of the pseudo force in the direction perpendicular to the surface of the wedge.