Question

In the system shown in figure ${M_1} > {M_2}$ and pulley and threads are ideal. System is held at rest by thread $BC$. Just after thread $BC$ is burnt.

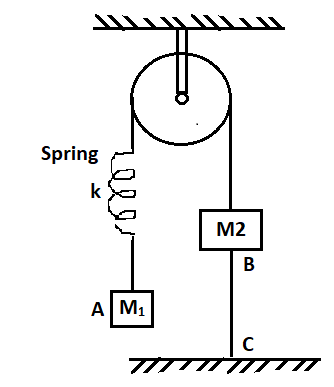
A) Acceleration ${M_1}$ and ${M_2}$ will be upward.
B) Magnitude of acceleration of both masses will be $\dfrac{{{M_1} - {M_2}}}{{{M_1} + {M_2}}}g.$
C) Acceleration of ${M_1}$ and ${M_2}$ will be equal to zero.
D) Acceleration of ${M_1}$ will be equal to zero, which that of ${M_2}$ will be $\dfrac{{{M_1} - {M_2}}}{{{M_2}}}g$ upward.

Answer 1

In order to solve this question you have to know the concept of pulley and tension in thread. A pulley is a simple machine that redirects force. Tension is the force that is transmitted through a string, rope, cable, or wire when it is pulled tight by forces acting from opposite ends.

Complete step by step solution:
In this question it is given that ${M_1} > {M_2}$, so the tension in the string connecting the block and surface is given by
${T_{BC}} = ({M_1} - {M_2})g$
It is also given in the question that the string BC is burnt, then this tension disappears and the tension in the spring becomes
${T_s} = {M_1}g$
The spring also gets elongated.
Now, the tension in the string connected to A and B is given by
${T_{AB}} = {M_1}g$
Hence, the resultant force on A becomes zero because the tension in string is balanced by spring tension.
Hence, the net force exerted on the block B which is upward in direction is given by
${F_B} = ({M_1} - {M_2})g$
So, the initial acceleration of the block B is given by
${u_B} = \dfrac{{({M_1} - {M_2})}}{{{M_2}}}g$
Thus, the initial acceleration of mass ${M_1}$ is zero
And the initial acceleration of mass ${M_2}$ is $\dfrac{{({M_1} - {M_2})}}{{{M_2}}}g$ and the direction is upward.

Thus, the correct option is (D).

Note: While solving questions like this we should always draw a free body diagram (FBD) to show the forces exerted on the body. Also, you have to make some assumptions while writing equations that the string is taut and inextensible at each and every point of time, the pulley is massless, and also the string is massless.