Question
Question: In the system shown in figure find the angular frequency of small oscillations of block of mass M. H...
In the system shown in figure find the angular frequency of small oscillations of block of mass M. Here pulley has moment of inertia I about horizontal axis passing through O. In equilibrium, line OA is horizontal
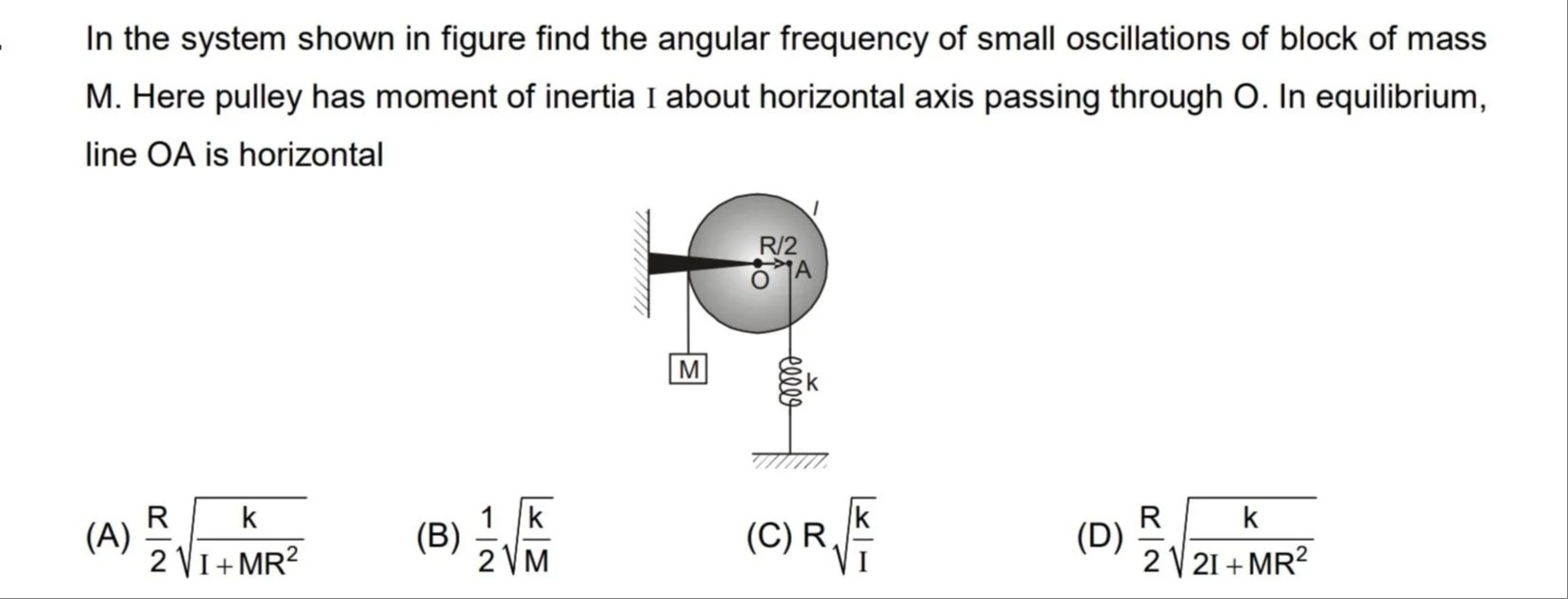
2RI+MR2k
21Mk
RIk
2R2I+MR2k
(A) 2RI+MR2k
Solution
We assume that the pulley has two different effective radii. In equilibrium the block hangs from the left rim (with effective radius R) while the spring is attached to the right at a point A which is a horizontal distance R/2 from O. (This is indicated by “line OA is horizontal” and the label “R/2”.) In equilibrium the torques balance: Block: Torque = Mg·R Spring: Torque = F_s·(R/2) Thus, F_s = 2Mg.
Now take a small rotation φ (with φ = 0 at equilibrium). Then:
- The block descends by an amount x = R·φ.
- The point A (spring attachment) moves vertically by Δy = (R/2)·φ.
The kinetic energies are: • Pulley (rotation): T₁ = ½ I φ̇² • Block (translation): T₂ = ½ M (R φ̇)² = ½ M R² φ̇²
Thus the total kinetic energy is T = ½ (I + M R²) φ̇².
The only quadratic (restoring) potential comes from the spring. Since a upward displacement of A by (R/2)φ reduces the spring’s extension (from its equilibrium value) by (R/2)φ, the change in the spring potential energy is V = ½ k[(Rφ/2)]² = (k R² φ²)/8.
Forming the Lagrangian L = T – V gives the small‐oscillation equation (I + M R²) φ̈ + (k R²/4) φ = 0. Thus the angular frequency for φ–oscillations is ω = √[(k R²/4)/(I + M R²)] = (R/2) √[k/(I + M R²)].
Since the block’s vertical displacement is directly related to φ by x = Rφ, its oscillation frequency is the same.
