Question

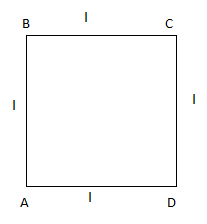
In the square frame of side l of metallic rods, corners A and C are maintained at ${T_1}$ and ${T_2}$​ respectively. The rate of heat flow from A to C is ω. If A and D are instead maintained at ${T_1}$ and ${T_2}$ respectively, the total rate of heat flow is $\left( {\dfrac{x}{3}} \right)\omega$. Find ‘x’.

Answer 1

The amount of heat transferred per unit of time in the material is called the rate of heat flow. The rate of heat flow depends on the conductivity of the material, the cross sectional area and the temperature difference between the objects.

Complete step by step solution:
Given data:
The Side of the square = l
The rate of heat flow from A to C = $\omega$
X =?
We know that thermal resistance, R is given by the formula,
$R = \dfrac{L}{{KA}}$
Where R is the resistance, L is the length of the conductor, K is thermal conductivity, and, A is the cross
Sectional area.
It is given that A and C are maintained at a temperature ${T_1}$ and ${T_2}$respectively. Thus we can consider that ${R_{AB}}$ and ${R_{BC}}$ are in series.
Thus ${R_{AC - upper}} = {R_{AB}} + {R_{BC}} = \dfrac{L}{{KA}} + \dfrac{L}{{KA}} = \dfrac{{2L}}{{KA}}$ and
${R_{AC - lower}} = {R_{AD}} + {R_{DC}} = \dfrac{L}{{KA}} + \dfrac{L}{{KA}} = \dfrac{{2L}}{{KA}}$
Thus ${R_{AC - upper}}$and ${R_{AC - lower}}$will be in parallel.
$\therefore \dfrac{1}{{{R_{AC}}}} = \dfrac{1}{{{R_{Ac - upper}}}} + \dfrac{1}{{{R_{AC - lower}}}}$
$\Rightarrow {R_{AC}} = \dfrac{L}{{KA}}$
Thus, ${\left( {\dfrac{{dQ}}{{dt}}} \right)_{AC}} = \dfrac{{{T_2} - {T_1}}}{{{R_{AC}}}} = \left( {{T_2} - {T_1}} \right)\dfrac{{KA}}{L} = \omega$
( $\because$ it is given that the rate of heat flow from A to C is $\omega$)
It is also given that A and D are maintained at a temperature ${T_1}$ and ${T_2}$respectively. Thus we can consider that ${R_{AB}}$ , ${R_{BC}}$, and, ${R_{CD}}$ are in series.
$\therefore {\dfrac{1}{{\left( {{R_{AD}}} \right)}}_{equ}} = \dfrac{{{R_{AB}} + {R_{BC}} + {R_{CD}}}}{{{R_{AD}}}}$
$\Rightarrow {\dfrac{1}{{\left( {{R_{AD}}} \right)}}_{equ}} = \dfrac{{\dfrac{L}{{KA}} + \dfrac{L}{{KA}} + \dfrac{L}{{KA}}}}{{\dfrac{L}{{KA}}}}$
$\Rightarrow {\left( {{R_{AD}}} \right)_{equ}} = \dfrac{{3L}}{{4KA}}$
Thus, ${\left( {\dfrac{{dQ}}{{dt}}} \right)_{AD}} = \dfrac{{{T_2} - {T_1}}}{{{{\left( {{R_{AD}}} \right)}_{equ}}}} = \dfrac{{\left( {{T_2} - {T_1}} \right)}}{{\dfrac{{3L}}{{4KA}}}} = \dfrac{4}{3}\omega$
( $\because$ it is given that the rate of heat flow from A to D is $\left( {\dfrac{x}{3}} \right)\omega$)
Thus, $x = 4$.

Note: 1. The flow which is caused due to the temperature difference between the two objects is called heat. It is represented by the letter Q and the unit is Joule.
2. When heat flows into the system, the heat flow will be positive and when heat flows out the system, the heat flow will be negative.