Question

In the space shown a non-uniform magnetic field $\vec B = B_{\circ}(1+x)(-\hat k)$T is present. A closed loop of small resistance is moving with a velocity ‘v’ as shown in the figure. The force due to magnetic field on the loop is:

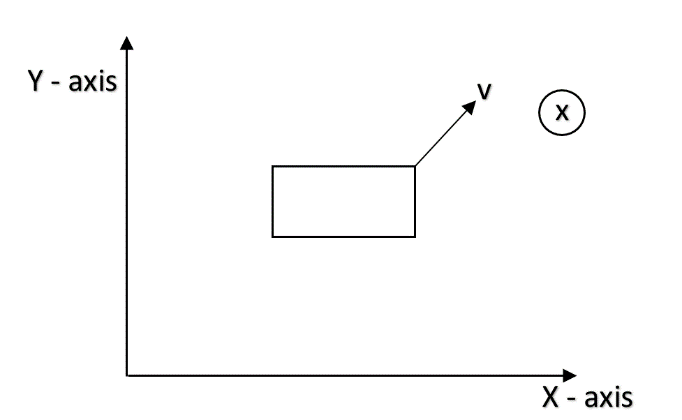
A. Zero
B. along – x direction
C. along + x direction
D. along + y direction.

Answer 1

Magnetic field is the space around the magnet where the effect of magnet can be felt by another magnet or iron piece. Magnetic flux is a quantity which defines the intensity of magnetic field passing per unit area. The S.I unit of magnetic field is Tesla (T) whereas the C.G.S unit is Gauss (G) and that of magnetic flux is Weber.

Complete answer:
According to Lenz law, the change in magnetic field is opposed in such a manner that the current inside the coil will resist the magnetic field by flowing in a particular direction.
Now the loop is moving in a non uniform magnetic field. This means the magnetic field linked with the loop will change or else flux will change. Also by the statement of Lenz law, we can understand that the change in flux will cause the loop to resist the change in flux and hence motion. So it will surely experience a force.
Now, we need to find in what direction the magnetic field is non uniform? As $\vec B = B_{\circ}(1+x)(-\hat k)$, so the magnetic field is the function of ‘x’ only. Also the magnetic field is increasing with the increase in ‘x’. Hence the force will be in such a direction that it will try to reduce the field and hence the loop wants to go in ‘-x’ direction. Hence it’ll experience force in ‘- x’ direction.

So, the correct answer is “Option B”.

Note:
This is only the case when the magnetic field is non uniform. Suppose the magnetic field to be constant. Then it won’t experience any force until the area is constant. This is because the flux linked with the wire per unit area will be constant and hence the loop won’t resist the motion.