Question

In the space shown a non-uniform magnetic field $\overrightarrow{B}={{B}_{\text{o}}}\left( 1+x \right)\left( -\hat{k} \right)$ tesla is present. A closed loop of small resistance placed in the x-y plane is given velocity ${{V}_{\text{o}}}$. The force due to magnetic field on the loop is

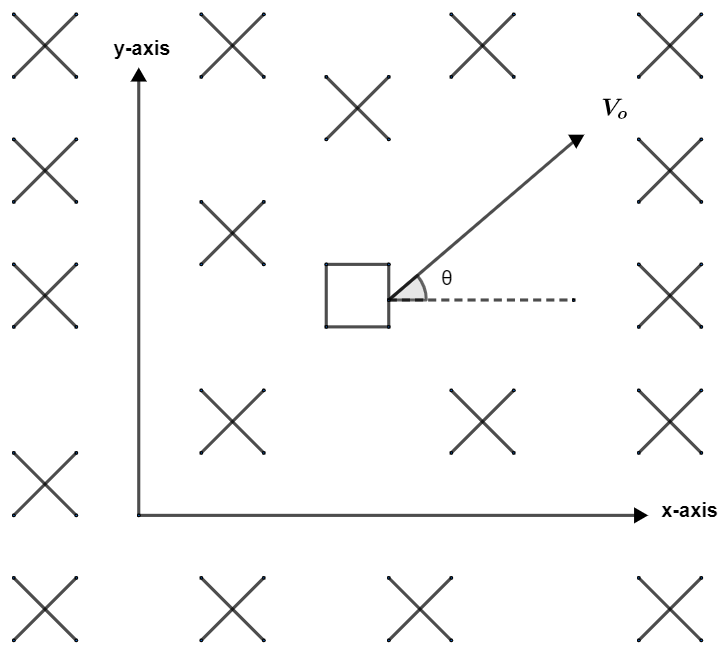
(a) Zero
(b) Along +x direction
(c) Along – x direction
(d) Along +y direction
(e) None of above

Answer 1

As the question discussed about a loop whose intensity of magnetic field is to be noticed so, it will be helpful to use the formula of Lenz’s law which is Faraday's equation’s modified version. After this we will notice its field by movement of loops in different directions.

Formula used:
$e.m.f.=-N\left( \dfrac{\Delta \phi }{\Delta t} \right)$ where e.m.f. is electro based electromotive force, $\Delta t$ is change in time and $\Delta \phi$ is variations in flux.

Complete answer:
Lenz’s law: By Lenz law we mean that any electro based force can generate current. This current further implies magnetic fields which resist variations created in magnetic flux. A formula by lenz’s is a modification of Faraday’s formula as $e.m.f.=-N\left( \dfrac{\Delta \phi }{\Delta t} \right)$

In the diagram given in question we can see that there is a non-uniform magnetic field all over. There is a loop which is completely enclosed also; it has very low power of opposition. This clearly lies in the x-y plane only. It has been moved with a velocity ${{V}_{\text{o}}}$. We are supposed to find the magnetic field that is generated around it. If we try an action of this loop moved into y direction then we will find that the magnetic field will remain constant there. Moreover, if we try an action of moving the loop in x direction then we get that the magnetic field actually changes. This is because of the change in flux created by electromotive force. Thus, by Lenz’s law we find that the current is now flowing which restricts the action of moving the loop in x direction.

So, the correct answer is “Option C”.

Note:
The formula of Lenz’s law is a must here as it includes flux with respect to time. If one knows the formula $e.m.f.=-N\left( \dfrac{\Delta \phi }{\Delta t} \right)$ then it will be easy to understand that these are directly proportional except for time. That is if electromotive forces are increased then there will be an increase in flux also. It is important to know the correct directions and the direction of the loop as to where the loop is moving. The one who will solve it in this way will be able to solve the question properly.