Solveeit Logo
Login

Question

Question: In the situation shown in the figure, the tension in the string connecting the two blocks will be (s...

In the situation shown in the figure, the tension in the string connecting the two blocks will be (string is massless and frictional force is negligible)

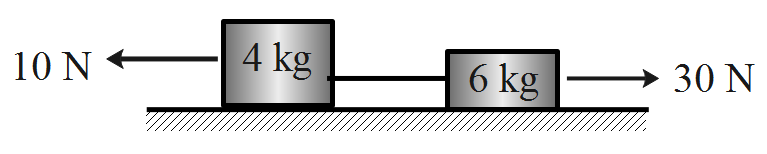
A. 20 N
B. 25 N
C. 30 N
D. 18 N

Explanation

Solution

The tension in the string is equal to the force of gravity, in turn, this force of gravity is equal to the product of the mass and acceleration due to gravity. As the tension in the string due to both of the blocks are acting in opposite directions, so, using these equations, we will compute the value of the tension in the string.

Complete step-by-step solution:
Consider the figure repressing the tension in the string due to the blocks.

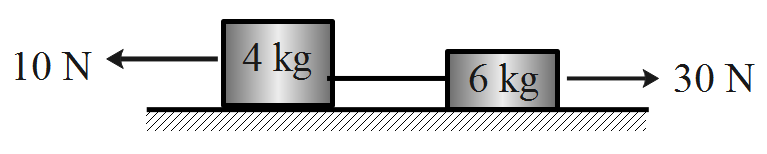
The tension and the force will be always working in opposite directions.
Consider the first block with a mass of 4 kg, so, we have the data as follows.
The tension in the string due to block of 4 kg, T
The amount of force acting in the opposite direction, 10 N.
The mass of the block, 4 kg.
The mathematical representation of the same is given as follows.
10−T=4F10-T=4F…… (1)
Consider the second block with a mass of 6 kg, so, we have the data as follows.
The tension in the string due to block of 6 kg, T
The amount of force acting in the opposite direction, 30 N.
The mass of the block, 6 kg.
The mathematical representation of the same is given as follows.
30−T=6F30-T=6F…… (2)
Solve the equations (1) and (2).
Thus, the force of gravity is, F=10 m/s2  F=10\,{m}/{{{s}^{2}}}\;
Consider the first equation to find the value of the tension in the string.

& 10-T=4F \\\ & \Rightarrow 10-T=4(10) \\\ & \therefore T=30N \\\ \end{aligned}$$ **$$\therefore $$ The tension in the string connecting the two blocks with the string being massless and considering the frictional force to be negligible is 30 N, thus, option (C) is correct.** **Note:** The tension in the string is different from that of the tension in the spring. The tension in the string is the product of the mass and the acceleration due to gravity, whereas, the tension in the spring is the product of the spring constant and the distance by which the spring got stretched or compressed.