Question
Question: In the situation shown blocks are connected with the help of ropes. Find \(\left( a \right)\) the ac...
In the situation shown blocks are connected with the help of ropes. Find (a) the acceleration of blocks and (b) Tension at the middle of each rope. Masses of blocks and ropes are indicated in the figure. (Takeg=10m/s2)
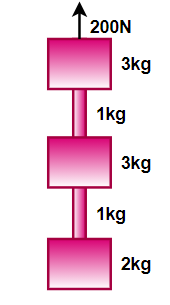
Solution
Here, in this question, we have to find the acceleration so as we know that the acceleration is equal to the force upon the mass. So by calculating the force we will be able to get the acceleration from there. For calculating the tension, we will equate the tension with the force and solve it to get the tension for each rope.
Formula used:
Acceleration,
Acceleration=AreaForce
Complete step by step answer:
(a) So as we know that force is equal to the product of mass and acceleration. Therefore, according to the question, the formula will become
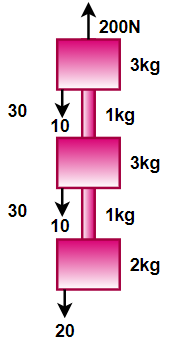
F−(mg)total=mtotal×a
Now by substituting the values, we will get the above equation as
⇒200−(40+40+20)=(5+3+2)×a
And on solving the above equation, we get
⇒200−(100)=10×a
Solving for the constant value, that is acceleration, we get the equation as
⇒a=10200−100m/s2
And on solving it,
⇒a=10m/s2
Therefore, the acceleration of the block is equal to 10m/s2 .
(b) Tension at the middle of each rope is named as T1andT2
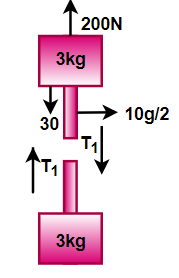
So, from the figure by equating the tension in the block, the equation will become
⇒200−30−5−T1=(3.5)×a
Since we already have calculated the values for the acceleration, so we get
⇒200−30−5−T1=(3.5)×10
Now on solving the LHS and RHS of the equation, we get
⇒175−T1=35
And on solving for the constant term that is the tension, we get the values as
⇒T1=130N
Similarly, for the second tension in the rope, we will follow the same procedure, but for this, we have to find T first, so we get the equation as
⇒T−30−10−20=(3+2+1)a
On substituting the values for the acceleration, we get the equation as
⇒T−30−10−20=(3+2+1)10
And on solving the LHS and RHS, we get
⇒T−60=60
Therefore, the value will become
⇒T=120N
Now we will find the second tension which is T2 , so the equation will become
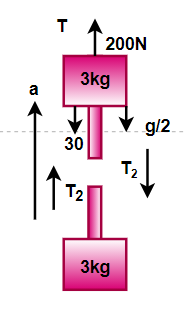
⇒T−30−2g−T2=(3+0.5)a
Now on substituting the known values, we get
⇒120−30−210−T2=(3+0.5)10
And on solving the LHS and RHS, we get
⇒120−30−5−T2=35
And on solving for the constant value, we get
⇒T2=120−35−35
And on solving it,
⇒T2=50N
Therefore, Tension in the middle of each rope is named as T1andT2 is equal to 130Nand50N respectively.
Note: The tension force is that type of force in which the transmission of force is done through a string, rope, cable, or wire when it is pulled tight by forces acting from opposite ends. And it will be focused along the length of the wire that gets pulled equally on the objects on the opposite ends of the wire.
