Question

In the shown pulley block system strings are light, pulleys are massless and smooth. System is released from rest.in 0.6 second [Take $g = 10\,m/{s^2}$ ] Find the following

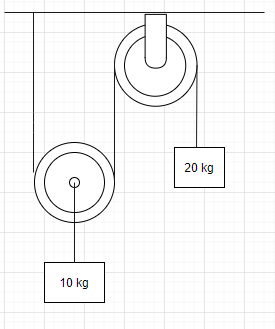
A. Work done on $20\,kg$ block by gravity
B. Work done on $20\,kg$ block by string
C. Work done on $10\,kg$ block by gravity
D. Work done on $10\,kg$ block by string

Answer 1

Hint-
For $10\,kg$ mass the force acting on it is force due to gravity mg acting downwards and tension T in two strings acting upward. Therefore, the net force ma can be written as
$2T - mg = ma$
Where a is the acceleration of the 10 kg mass
For $20\,kg$ mass the forces acting on it are force of gravity mg downwards and force due to tension T upwards. If acceleration of 10 kg block is taken as a, then acceleration of 20 kg block will be twice.
So, the net force can be given as
$\,mg - T = m \times 2a$
Work is force times displacement.
Work done by gravity is given as
$W = mgh$
The value of h can be found out using
$S = ut + \dfrac{1}{2}a{t^2}$
Where u is the initial velocity, t is the time and a is the acceleration.
Here the initial velocity is 0.
Work done by string on 20 kg mass is given as
$W = - T \times h$
Where h is the displacement.
Work done by gravity on 10 mass is given as
$W = - mg(h/2)$
Work done by string on $10\,kg$ mass is given as
$W = 2T \times \dfrac{h}{2}$

Step by step solution:
In the given system we can see that.
For $10\,kg$ mass the force acting on it is force due to gravity mg acting downwards and tension T in two strings acting upward. Therefore, the net force ma can be written as
$2T - mg = ma$
$2T - 10g = 10a$
Where a is the acceleration of the 10 kg block
For $20\,kg$ mass the forces acting on it are force of gravity mg downwards and force due to tension T upwards. If acceleration of 10 kg block is taken as a, then acceleration of 20 kg block will be twice.
So, the net force can be given as
$\,mg - T = m \times 2a$
$\,20g - T = 20 \times 2a$
Solving these two equations for a we get
$a = \dfrac{g}{3}$
Let the $20\,kg$mass be at a height h. The value of h can be found out using
$S = ut + \dfrac{1}{2}a{t^2}$
Where s is the displacement, u is the initial velocity, t is the time and a is the acceleration
Initial velocity is zero. Thus,
$h = \dfrac{1}{2}a{t^2}$
$\Rightarrow h = \dfrac{1}{2}\dfrac{g}{3}{t^2}$
$\Rightarrow h = \dfrac{1}{2}\dfrac{{10\,m/{s^2}}}{3}{\left( {0.6\,s} \right)^2}$
$\therefore h = \dfrac{6}{{10}}\,m$
Work done is force times displacement.
Now work done by gravity on $20\,kg$mass is given as
$W = mgh$
On substituting the values we get,
$W = 20\,kg \times 10\,m/{s^2} \times \dfrac{6}{{10}}\,m$
$\therefore W = 120J$
Work done by string on 20 kg mass is given as
$W = - T \times h$
From equation (1) Tension $T = \dfrac{{10g - 10a}}{2}$
$T = \left( {\dfrac{{10g - 10g/3}}{2}} \right)$
$\Rightarrow T = \dfrac{{\left( {\dfrac{{20g}}{3}} \right)}}{2}$
$\therefore T = \left( {\dfrac{{100}}{3}} \right)N$
Therefore, work done by string
$W = - \left( {\dfrac{{100}}{3}} \right)N \times \dfrac{6}{{10}}\,m$
$\therefore W = - 20\,J$
Work done by gravity on 10 mass is given as
$W = - mg(h/2)$
$\Rightarrow W = - 10 \times 10 \times \left( {\dfrac{6}{{20}}} \right)$
$\therefore W = 30J$
Work done by string on $10\,kg$ mass is given as
$W = 2T \times \dfrac{h}{2}$
$\Rightarrow W = T \times h$
$\therefore W = 20\,J$

Note: Work done can be both positive and negative. While calculating work always remember to consider the direction in which force and displacement take place. If displacement is not along the direction of force then the work done should be taken as negative. If the displacement is in the direction of force then work done will be positive.
While calculating the work due to tension we used a negative sign for the $20\,kg$ because tension there is acting upward but the block is moving downward. So, the work done by tension is negative there. Where as in the case of $10\,kg$ mass the total force $2\,T$ acts upward and the direction of motion of the block is also upward. So, there the work done by tension is positive work.