Question
Question: In the shown arrangement of two blocks and two light strings 1 and 2, if \(\Delta {l_1}\) and \(\Del...
In the shown arrangement of two blocks and two light strings 1 and 2, if Δl1 and Δl2 are elongation in the string 1 and 2 respectively, then
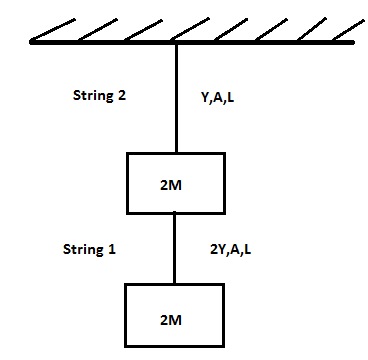
A. Δl1=YA4mgL
B. Δl2=2Δl1
C. Δl2=YA4mgL
D. Δl1=4Δl2
Solution
In the figure, we can see that two blocks are hanging vertically with one side hinged. Here, we have to analyze how and which force is acting on the two strings. As the variables are given, we just have to put the values in Young’s modulus formula to achieve the desired relationship between the two elongations. The force is applied vertically so that the strings get elongated by a small length.
Complete step by step answer:
The ratio of tensile stress to tensile strain is known as Young’s modulus. It tells about the amount of compression or elongation a material can withstand with respect to its length. It's S.I. unit is Pascal. Mathematically it is represented as:
⇒Y=(Δl/l)(F/A).......(1)
Where,
Y is Young’s modulus.
Fis the force exerted by a body when it experiences tension.
A is the area of cross-section
l is the original length.
Δl is the change in length.
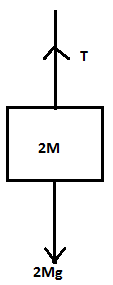
Now, we have to use these formulas to get our answer. Let us consider String 1 given in the figure. The first thing we have to find is the force acting on string 1. As a mass of 2M is suspended to it, it experiences tension and only acceleration due to gravity, ‘g ‘ acts on it as the system is not moving. We can see this using a free body diagram as shown:
We know that,
Force, F=ma
Where,
F is the force.
m is the mass of the body.
a is the acceleration of the body.
Now we have to solve the free body diagram. There is no acceleration in the system, therefore, a=0 . Therefore,
⇒F=T−2Mg
As acceleration is zero, the force will also be zero, hence we get,
⇒T=2Mg
Here, T is the tension in string 1 and hence is the required force. Using equation (1), we get,
⇒Y=(Δl/l)(F/A)
⇒Δl=YAFl.........(2)
In the question it is given that the length of string 1 is ‘L ‘, the area of cross-section is ‘A’ and Young’s modulus is ‘2Y’. Putting these values in equation (2) we get the elongation in string 1 as:
⇒Δl1=2YA2mgL
⇒Δl1=YAmgL --- 3
Similarly, we can draw the free body diagram with string 2 which is the same as before. Here also tension force,T=2Mg . The length of string 2 is ‘L ‘, the area of cross-section is ‘A’ and Young’s modulus is ‘Y’. Putting these values in equation (2) we get the elongation in string 2 as:
⇒Δl2=YA2mgL --- 4
To get the relation between the two elongations, we have to use equation (3) and equation (4), we get,
⇒Δl2=YA2mgL
⇒Δl2=2Δl1
Therefore, option B is the correct answer.
Note: Whenever an object is subjected to an external force, it experiences deformation that is changed in its dimensions. When the force is applied along the axis of force, it stretches the material. Such an external force acting per unit area resulting in the elongation of the material is called tensile stress. The SI unit of tensile stress is Pascal. It can be defined as the ratio of the force applied along the string to the area of cross-section of the string that is perpendicular to the applied force.
Tensile stress,
⇒σ=AF
Where,
σ is tensile stress.
Fis the force exerted by a body when it experiences tension.
A is the area of cross-section.
Tensile Strain is defined as the ratio of the change in the dimension of an object due to tensile stress to its original dimension. It is a dimensionless quantity.
Tensile strain,
⇒ε=lΔl
Where,
ε is the tensile strain.
Δl is the change in length.
l is the original length.
