Question

In the resonance tube experiment the length of an air column is 1m and it vibrates with a tuning fork of frequency ‘n’. If it is to vibrate with a frequency of ‘$\dfrac{4}{3}$ n’, increase in the height of water in the tube must be
a) $25$ cm
b) $50$ cm
c) $75$ cm
d) $100$ cm

Answer 1

The above experiment can be considered as a closed cylindrical pipe, which is closed at one end and open on its other side. Hence we can use the condition we can use for a pipe closed at one end to determine the increase in height.

Complete answer:
The fundamental frequency of the first harmonic for a pipe open at one end is given by,
${{v}_{1}}=\dfrac{\overline{v}}{4L}$
(Let us call the above expression as equation 1)
Now let us understand quantities in the expression,
${{v}_{1}}$ is the first fundamental frequency
$\overline{v}$ is the speed of the sound in air
$L$ is the length of the air column.
Using the data from the question, first we will calculate $\overline{v}$
$\begin{aligned} & \because L=1m \\\ & {{v}_{1}}=n \\\ \end{aligned}$
Equation 1 can be written as,
$n=\dfrac{\overline{v}}{4(1)}$

After simplifying by cross multiplication the above expression reduces to,
$\overline{v}=4n$
To find the increase in the height of the water tube we must first determine the length of the resonating column for a frequency =‘$\dfrac{4}{3}$ n’. Again using the first fundamental frequency expression,
${{v}_{1}}=\dfrac{\overline{v}}{4L}$
$\because \overline{v}=4n$ and ${{v}_{1}}=\dfrac{4n}{3}$
$\begin{aligned} & \dfrac{4n}{3}=\dfrac{4n}{4L} \\\ & \\\ & L=\dfrac{3}{4}m \\\ & \\\ & L=75cm \\\ \end{aligned}$

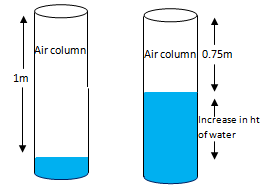
From the above diagram increase in the height of water is,
Air column of the 1 - Air column of the 2
$\begin{aligned} & 1-0.75=0.25m \\\ & 25cm \\\ \end{aligned}$
Hence the correct answer to the question is option a.

Note:
We should always consider the first harmonic condition whenever it’s not mentioned in the question. Do not use the condition of the second or third harmonic as the question consists of the fundamental mode. The first harmonic means a periodic wave function whose functional form is sine or cosine. For a open end pipe only odd harmonics are present i.e. first harmonic (${{v}_{1}}$ ), second harmonic ($3{{v}_{1}}$ ) till n ${{v}_{1}}$, where n is odd.