Question
Question: In the rectangle \(ABCD\), what is the area of \(\Delta BEF\) in terms of \(x,y,z\) ? 
Solution
First, we will find the length of all the sides and then compute the area of all triangles and the rectangle ABCD , by solving all these equations and areas we will get the area of ΔBEF in terms of x,y,z .
Complete answer:
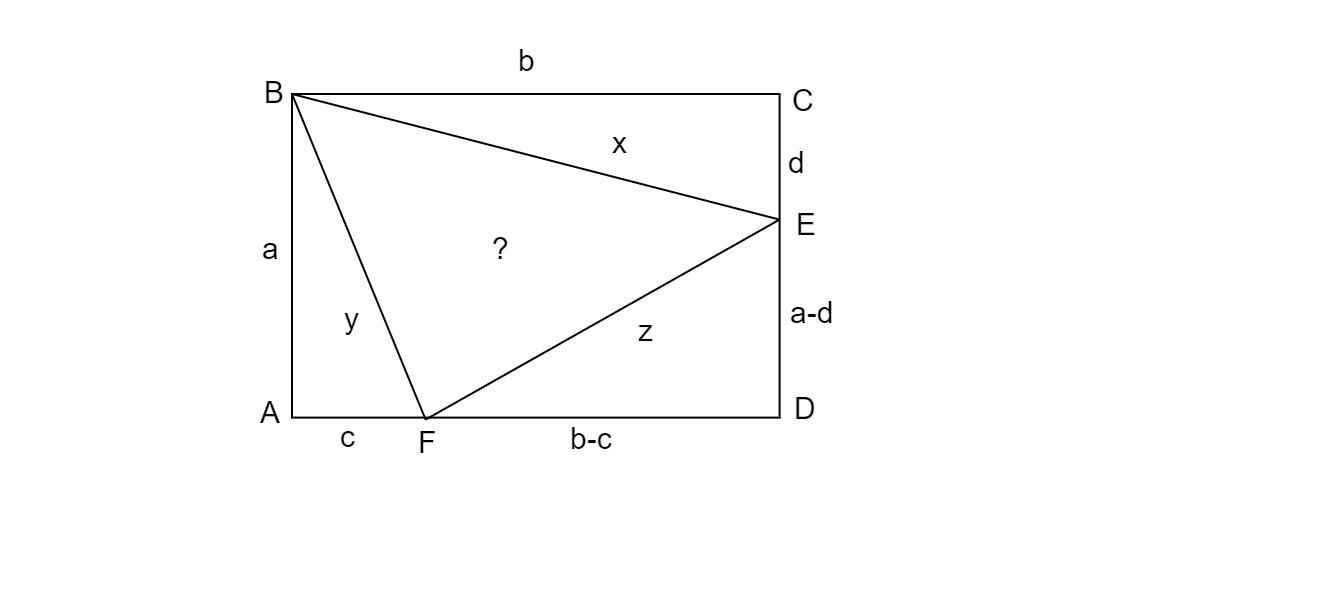
Let us assume the length of sides AB=a,BC=b,AF=c,CE=d respectively.
Area of triangle = 21×base×height
Consider ΔABF,
⇒ Area of ΔABF = y …. (Given)
21×a×c=y
c=a2y
Consider ΔBCE,
Area of ΔBCE = x …. (Given)
21×b×d=x
d=b2x
side BC=side AD=b …. (Opposite side of rectangle are congruent)
side AB=side CD=a …. (Opposite side of rectangle are congruent)
⇒ sideAD=sideAF+sideFD …. (A−F−D)
b=c+sideFD
∴sideFD=b−c=b−a2y
⇒ sideCD=sideCE+sideED …. (C−E−D)
a=d+sideED
∴sideED=a−d=a−b2x
Consider ΔDEF,
Area of ΔDEF = z …. (Given)
⇒ 21×(b−a2y)×(a−b2x)=z
⇒ ab−2x−2y+ab4xy=2z
⇒ ab−2x−2y−2z+ab4xy=0
Multiplying both sides by ab we get,
⇒ (ab)2−2(ab)(x+y+z)+4xy=0
This equation is a quadratic equation of form ax2+bx+c=0 and the roots of the equation are given by x=2a−b±b2−4ac
Here, x=ab,a=1,b=−2(x+y+z),c=4xy
∴ab=2(1)−(−2(x+y+z))±(−2(x+y+z))2−4(1)(4xy)
∴ab=22(x+y+z)±4(x+y+z)2−16xy
∴ab=22(x+y+z)±4[(x+y+z)2−4xy]
Taking 4 common and inside the radical symbol and taking it out the radical sign we have,
∴ab=22(x+y+z)±2(x+y+z)2−4xy
Taking 2 common in the numerator, we have:
∴ab=22[(x+y+z)±(x+y+z)2−4xy]
cancelling 2, then we have,
∴ab=(x+y+z)±(x+y+z)2−4xy
The area of rectangle ABCD = base×height=a×b=ab
Substituting the value of ab which we got by solving the quadratic equation, we get,
Area of rectangle ABCD = base×height=a×b=ab=(x+y+z)±(x+y+z)2−4xy
Consider the area of ΔBEF=ω,
Therefore, we can say
Area of rectangle ABCD = area of ΔABF+ area of ΔBCE + area of ΔDEF+ area of ΔBEF
Substituting all the values we got into this equation we get,
⇒ ab=x+y+z+ω
∴(x+y+z)±(x+y+z)2−4xy=(x+y+z)+w
Since, ab is the area of entire rectangle, it is larger than (x+y+z) and hence we can reject the negative radical and consider only positive radical,
⇒ w=(x+y+z)2−4xy
⇒ ΔBEF=ω=(x+y+z)2−4xy
Therefore, the area of ΔBEF in terms of x,y,z is (x+y+z)2−4xy .
Note:
Consider the sides of the rectangle and triangle as some constants and then form equations and find the solution of those equations. The area of a triangle inside a rectangle always has an area less than that of the rectangle.
