Question
Question: In the pulley system shown in the figure, the movable pulleys A, B and C are mass 1 kg each. D and E...
In the pulley system shown in the figure, the movable pulleys A, B and C are mass 1 kg each. D and E are fixed pulleys. The strings are light and inextensible. Find the tension in the string.
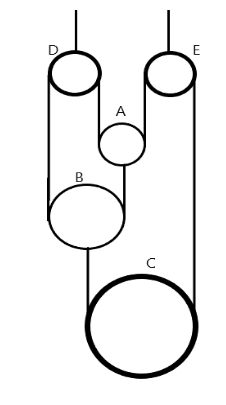
Solution
All strings are connected together, hence the tension in the strings are all equal. We need to apply Newton’s second law on each of the movable pulleys. Since the string is inextensible, then the total length is constant through any motion that may occur. Use this as a constraint equation.
Formula used: In this solution we will be using the following formulae;
Fnet=ma where Fnet is the net force acting on a body, m is the mass of the body and a is the acceleration of the body.
Complete Answer:
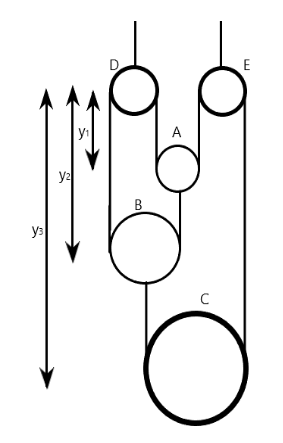
As seen from the diagram, the total length of wire can be given as
l=y3+y1+y1+(y2−y1)+y2+(y3−y2)
By simplifying, we have
l=2y3+y2+y1
Now, differentiating the above equation twice, we have
2dt2d2y3+dt2d2y2+dt2d2y1=0
⇒2a3+a2+a1=0
Now, applying Newton’s second law on the movable pulleys, we have
On pulley A:
2T−(mg+T)=ma
⇒T−g=a1 (since m is equal to 1 kg)
Similarly on pulley B:
2T−(mg+T)=ma2
⇒T−g=a2 (since m is equal to 1 kg)
On pulley C,
2T−g=a3 (since m is equal to 1 kg)
Now, subtracting T−g=a2 from T−g=a1 , we get
a1−a2=0
a1=a2=a
Then putting the above into 2a3+a2+a1=0 , we get
2a3+a+a=0
a3=−a
Hence, from T−g=a1 and 2T−g=a3 , we have
T−g=a and 2T−g=−a respectively.
Adding the two equations, we get
3T−2g=0
Which implies that
T=32g
If we assume the acceleration due to gravity to be 10m/s2 , then we get
T=32(10)=320=6.67N.
Note:
For clarity, generally, constraint equations are equations that give information on what is allowed in the system. They can give information or derived from information about the degree of freedom, whether extension is allowed, or rolling is possible etc. And they are used to find the relation of the parameters to one another. For example, in the above, it was able to give information how the accelerations of the three pulley are related to one another
