Question

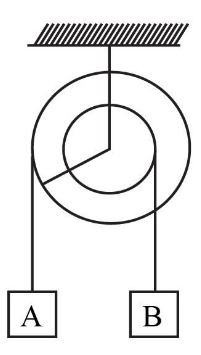
In the pulley system shown in the figure, if radii of bigger and smaller pulley are $2\;{\rm{m}}$ and $1\;{\rm{m}}$ respectively and acceleration of block A is $5\;{\rm{m/}}{{\rm{s}}^{\rm{2}}}$in the downward direction, then the acceleration of block B will be,

A. $0\;{\rm{m/}}{{\rm{s}}^{\rm{2}}}$
B. $5\;{\rm{m/}}{{\rm{s}}^{\rm{2}}}$
C. $10\;{\rm{m/}}{{\rm{s}}^{\rm{2}}}$
D. ${\rm{5/2}}\;{\rm{m/}}{{\rm{s}}^{\rm{2}}}$

Answer 1

In the solution we will use the relation between the linear acceleration and angular acceleration. Also, there is no need to draw a free body diagram and calculate the force acting on both the blocks. We will also use the concept of a rotating body about a fixed axis in which each particle has the same angular velocity and angular acceleration.

Complete step by step answer:
Given:
The radius of the smaller pulley is, $r = 1\;{\rm{m}}$.
The radius of the bigger pulley is,$R = 2\;{\rm{m}}$
The acceleration of block A is,${a_{\rm{A}}} = 5\;{\rm{m/}}{{\rm{s}}^{\rm{2}}}$
The relation between linear and angular acceleration is,
$a = \alpha r$
Angular acceleration of block A is,
${\alpha _{\rm{A}}} = \dfrac{{{a_{\rm{A}}}}}{R}$ … (i)
Angular acceleration of block B is,
${\alpha _{\rm{B}}} = \dfrac{{{a_{\rm{B}}}}}{r}$ … (ii)
As both the pulleys are pivoted at the same point and connected to each other, thus both the pulleys have the same angular velocity and angular acceleration.
${\alpha _{\rm{A}}} = {\alpha _{\rm{B}}}\\\ \Rightarrow\dfrac{{{a_{\rm{A}}}}}{R} = \dfrac{{{a_{\rm{B}}}}}{r}$
Rearranging the above terms,
${a_{\rm{B}}} = \dfrac{{{a_{\rm{A}}}r}}{R}$
Substitute the necessary values and calculate the linear acceleration of block B,
${a_{\rm{B}}} = \dfrac{{\left( {5\;{\rm{m/}}{{\rm{s}}^{\rm{2}}}} \right) \cdot \left( {1\;{\rm{m}}} \right)}}{{2\;{\rm{m}}}}\\\ \therefore {a_{\rm{B}}} = \dfrac{5}{2}\;{\rm{m/}}{{\rm{s}}^{\rm{2}}}$

Thus, the acceleration of block B is $\dfrac{5}{2}\;{\rm{m/}}{{\rm{s}}^{\rm{2}}}$. Hence option D is the correct answer.

Note: Make sure to use the concept of rotational motion that both the pulleys have the same acceleration to get the appropriate result and also remember that the linear acceleration of both the blocks are depend upon the distance of block from the pivoted point thus block A have more linear acceleration than block B.