Question
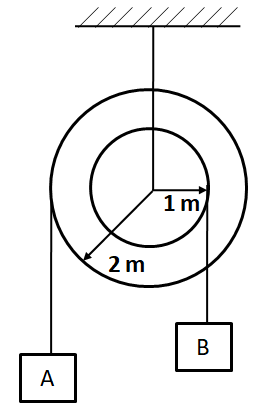
Question: In the Pulley system shown, if the radii of the bigger and smaller pulley are \( 2m \) and \( 1m \) ...
In the Pulley system shown, if the radii of the bigger and smaller pulley are 2m and 1m respectively, and the acceleration of the block A is 5m/s2 in the downward direction, the acceleration of block B will be:-
(A) 0m/s2
(B) 5m/s2
(C) 10m/s2
(D) 25m/s2
Solution
Hint To solve this question, we need to use the concept of the constrained motion. We have to find the angular acceleration of the rotating pulley, with the help of which the velocity of block B will be obtained.
Formula Used: The formula used to solve this question is given by
⇒a=αr , where a is the linear acceleration, α is the angular acceleration, and r is the radius.
Complete step by step answer
Let the acceleration of the block B be a2 .
We begin by finding the angular acceleration of the pulley. It is given that the block A, which is attached to the bigger pulley of radius 2m , has an acceleration of 5m/s2 . Since, the string connecting the block to the pulley is tangential with it, so we can say that this is the tangential acceleration of the block A, which is related to the angular acceleration of the bigger puller by
⇒a1=αr1
According to the question, r2=2m
⇒5=2α
Dividing by 2 we get
⇒α=25rad/s2 …………………….(1)
Now, since the smaller pulley of radius 1m is connected to the bigger pulley, so it will be constrained to rotate with the same angular acceleration of α=25rad/s2 . So, the linear acceleration of the block B, which is connected through the string to the smaller pulley, is given by
⇒a2=αr2
According to the question r1=1m . So we have
⇒a2=α
From (1) we finally get
⇒a2=25m/s2
Thus, the acceleration of block B is equal to 25m/s2 .
Hence, the correct answer is option D.
Note
Do not try to use Newton's laws of motion to solve this question. In pulley problems, use of NLM is very common. But this is the problem of constrained motion, where we do not consider the forces acting on the system. So use of Newton’s laws will not work here.
