Question

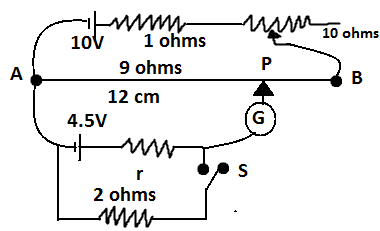
In the primary circuit of a potentiometer, the rheostat can be varied from 0-10 ohms. Initially it is at minimum resistance (zero). Find the length AP in meters of the wire such that the galvanometer shows zero deflection.

Answer 1

The galvanometer shows zero deflection only when no current passes through it. When the ratios of resistances on both sides of the galvanometer are equal, then no current flows through it.

Complete solution:
Potentiometer works on the principle of wheatstone bridge.
Wheatstone bridge:
A Wheatstone bridge is an electrical circuit used to measure an unknown electrical resistance by balancing two legs of a bridge circuit, one leg of which includes the unknown component. The primary benefit of the circuit is its ability to provide extremely accurate measurements. Its application is similar to that of potentiometer.

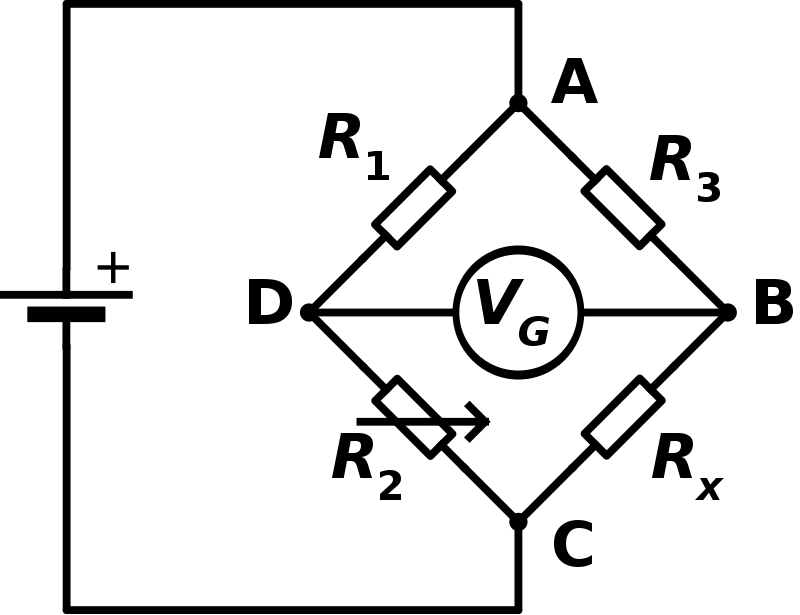
Mathematically for a Wheatstone bridge;
If, $\dfrac{{{R_1}}}{{{R_2}}} = \dfrac{{{R_3}}}{{{R_x}}}$, the no current passes through the galvanometer in the middle branch, i.e. current through ${V_G}$ is zero.
Now initially when the rheostat will have resistance as 0 ohms and galvanometer shows zero deflection we have;
${I_{AB}} = \dfrac{V}{{{R_{eq}}}}$
Here ${I_{AB}}$ is the total current is the circuit. As there is no current flowing through the galvanometer the only circuit to be considered is the upper circuit. So, the equivalent resistance for that circuit is ${R_{eq}} = 9 + 1 = 10\Omega$.
And the voltage across the circuit is V= 10V.
So, ${I_{AB}} = \dfrac{V}{{{R_{eq}}}}$
${I_{AB}} = {I_{AP}} = \dfrac{{10}}{{10}} = 1Amp$.
Also, potential drop across AP can be given by ${V_{AP}} = {I_{AP}}\rho l$.
Here, $\rho$is the resistance per unit length and l is the length of AP or balanced length of potentiometer.
Also since no current flows through the galvanometer the potential difference across AP will be ${V_{AP}} = 4.5V$.
Hence, we get;
$4.5 = {I_{AP}}\rho l$
Here, ${I_{AP}} = 1A$, $\rho = \dfrac{9}{{12}}\Omega {m^{ - 1}}$ and l=length of AP or balanced length of the potentiometer.
Thus, $4.5 = 1 \times \dfrac{9}{{12}}l$
$l = 4.5 \times \dfrac{4}{3} = 1.5 \times 4$
Hence, $l = 6m$.

Therefore the length of AP is 6 meters.

Note: Be careful if you are redrawing the circuit into a similar Wheatstone circuit. Chances of miss placing the resistors are very high.
Marking potential at each joint will help you redraw the circuit without any errors.
Knowledge of circuit diagrams and current electricity is must for solving such questions.