Question
Question: In the potentiometer circuit shown in figure, the internal resistance of the \(12V\) battery is \(1\...
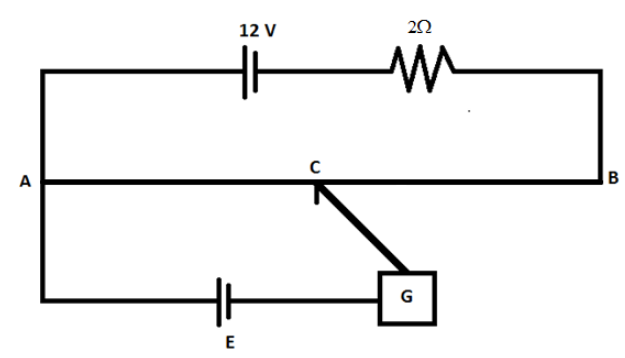
In the potentiometer circuit shown in figure, the internal resistance of the 12V battery is 1Ω and length of the wire AB is 100cm. When CB is 60cm. The galvanometer shows no deflection. The emf of cell E is (the resistance of wire AB is 3Ω)
A. 3.6V
B. 2.4V
C. 3V
D. 4.5V
Solution
In this question, we need to determine the emf of cell E such that the internal resistance of the 12V battery is 1Ω and length of the wire AB is 100cm. When CB is 60cm. For this, we will first find the value of current and the resistance then, substitute the value in the relation between the emf, current and the resistance to find the E.M.F. of the cell E.
Formula Used:
E.M.F.=I×R
Here I is the current and R is the resistance.
Complete step by step answer:
We have been given a potentiometer circuit diagram.In the given circuit diagram, the 12V battery has an internal resistance of 1Ω.Also, the wire AB is 100cm long.When the length of CB is 60cm, the galvanometer shows no deflection.We are also given that the resistance of wire AB is 3Ω.Now, we need to find out the E.M.F. of the cell E.The current is equal to the voltage divided by the sum of the external resistance, the internal resistance of the battery and the resistance of wire AB. This can be given as,
I = \dfrac{{12}}{{2 + 1 + 3}} \\\
\Rightarrow I = \dfrac{{12}}{6} \\\
\Rightarrow I = 2A \\\
Here, 12 is the voltage, 2 is the external resistance in the circuit, 1 is the internal resistance of the battery, and 3 is the resistance of wire AB.
Now, the E.M.F. of the cell E is equal to the potential difference across the section AC.
E.M.F = I \times R \\\
\Rightarrow E.M.F = 2 \times R \\\
For 100cm, R=3Ω.
As AC=60cm, R=100120Ω.
Therefore, the E.M.F. of cell E is equal to,
E.M.F.=I×R ⇒E.M.F.=2×100120 ∴E.M.F.=2.4V
Therefore, now we can conclude that the E.M.F. of the cell E is 2.4V.
So, option B is the correct answer.
Note: It is very important to note here that the galvanometer will show zero deflection when there is no flow of current through it. In other words, when there is equal voltage drop across the terminals of the galvanometer then, the galvanometer is said to have zero defection.
